题目内容
定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1)都有:f(x)+f(y)=f(
); ②当x∈(-1,0)时,f(x)>0,回答下列问题.
(1)证明:函数f(x)在(-1,1)上的图象关于原点对称;
(2)判断函数f(x)在(0,1)上的单调性,并说明理由.
(3)证明:f(
)+f(
)+…+f(
)>f(
),(n∈Z).
| x+y |
| 1-xy |
(1)证明:函数f(x)在(-1,1)上的图象关于原点对称;
(2)判断函数f(x)在(0,1)上的单调性,并说明理由.
(3)证明:f(
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| n2+3n+3 |
| 1 |
| 2 |
分析:(1)判断函数f(x)的奇偶性:①判断函数定义域是否关于原点对称,②判断f(-x)与f(x)的关系;
(2)证明函数f(x)的单调性,利用定义,分五步①设元,②作差,③变形,④判号,⑤下结论;
(3)利用题中所给的等式,把要求的与已知的相结合,将f(
)+f(
)+…+f(
)转化成f(
)-f(
),然后根据单调性可判断符号,从而得到结论.
(2)证明函数f(x)的单调性,利用定义,分五步①设元,②作差,③变形,④判号,⑤下结论;
(3)利用题中所给的等式,把要求的与已知的相结合,将f(
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| n2+3n+3 |
| 1 |
| 2 |
| 1 |
| n+2 |
解答:解:(1)令x=y=0,则2f(0)=f(0)即f(0)=0,
令y=-x,则f(x)+f(-x)=0,即f(-x)=-f(x),
∴函数f(x)在(-1,1)上是奇函数;
(2)设0<x1<x2<1,则f(x1)-f(x2)=f(x1)+f(-x2)=f(
),
而x1-x2<0,1+x1x2>0⇒
<0⇒f(
)>0,
即当x1<x2时,f(x1)>f(x2),
∴f(x)在(0,1)上单调递减;
(3)f(
)=f[
]=f[
]
=f[
]=f(
)+f(-
)=f(
)-f(
),
∴f(
)+f(
)+…+f(
)
=[f(
)-f(
)]+[f(
)-f(
)]+…+[f(
)-f(
)]
=f(
)-f(
),
∵0<
<1,且f(x)在(0,1)单调递减,
∴f(
)<f(0)=0,
∴f(
)-f(
)>f(
),
∴f(
)+f(
)+…+f(
)>f(
).
令y=-x,则f(x)+f(-x)=0,即f(-x)=-f(x),
∴函数f(x)在(-1,1)上是奇函数;
(2)设0<x1<x2<1,则f(x1)-f(x2)=f(x1)+f(-x2)=f(
| x1-x2 |
| 1+x1x2 |
而x1-x2<0,1+x1x2>0⇒
| x1-x2 |
| 1+x1x2 |
| x1-x2 |
| 1+x1x2 |
即当x1<x2时,f(x1)>f(x2),
∴f(x)在(0,1)上单调递减;
(3)f(
| 1 |
| n2+3n+3 |
| 1 |
| (n+1)(n+2)+1 |
| ||
1+
|
=f[
| ||||
1-
|
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴f(
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| n2+3n+3 |
=[f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=f(
| 1 |
| 2 |
| 1 |
| n+2 |
∵0<
| 1 |
| n+2 |
∴f(
| 1 |
| n+2 |
∴f(
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| 2 |
∴f(
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| n2+3n+3 |
| 1 |
| 2 |
点评:本题考查了抽象函数的奇偶性,单调性,与具体函数的证明方法相同,做题一定要抓牢定义,特别是证明题,一切方法源根本.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.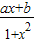 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.