题目内容
如图,已知点P是正方形ABCD所在平面外一点,PA⊥平面ABCD,PA=AB,点E、F分别在线段PB、AC上,满足BE=CF.
(1)求PD与平面ABCD所成的角的大小;
(2)求平面PBD与平面ABCD所成角的正切值.
(3)求证:EF⊥CD.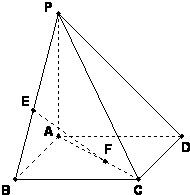
(1)求PD与平面ABCD所成的角的大小;
(2)求平面PBD与平面ABCD所成角的正切值.
(3)求证:EF⊥CD.

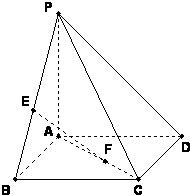
(1)∵PA⊥平面ABCD,
∴∠PDA是PD与平面ABCD所成角
又PA=AB=AD
∴∠PDA=45°,
∴PD与平面ABCD所成的角为45°
(2)连接BD交AC于O,连接PO,
则AC⊥BD,
∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,而PA∩AC=A,
∴BD⊥面PAC,又PO?面PAC,
∴BD⊥PO,
∴∠AOP就是平面PBD与平面ABCD所成角,
在Rt△AOP中,tan∠AOP=
| PA |
| AO |
| 2 |
(3)过点E作EH∥PA,交AB于H,连接FH,
则
| BE |
| BP |
| BH |
| BA |
∵BE=CF,BP=AC,∴
| BE |
| BP |
| CF |
| AC |
| BH |
| BA |
| CF |
| CA |
∴FH∥AD,
∵AD⊥CD,∴CD⊥FH 又PA⊥CD,∴CD⊥EH
∴CD⊥平面EFH,
∴EF⊥CD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目