题目内容
(理)(本题满分14分)如图,已知直线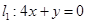 ,直线
,直线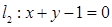 以及
以及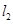 上一点
上一点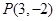 .
.
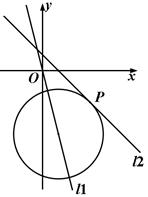
(Ⅰ)求圆心M在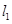 上且与直线
上且与直线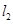 相切于点
相切于点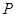 的圆⊙M的方程.
的圆⊙M的方程.
(Ⅱ)在(Ⅰ)的条件下;若直线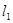 分别与直线
分别与直线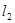 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点,
求证: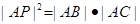 .
.
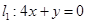 ,直线
,直线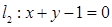 以及
以及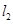 上一点
上一点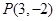 .
.
(Ⅰ)求圆心M在
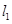 上且与直线
上且与直线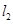 相切于点
相切于点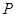 的圆⊙M的方程.
的圆⊙M的方程.(Ⅱ)在(Ⅰ)的条件下;若直线
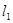 分别与直线
分别与直线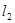 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点,求证:
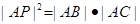 .
. (1)  (2)利用切割线定理来证明。
(2)利用切割线定理来证明。
 (2)利用切割线定理来证明。
(2)利用切割线定理来证明。试题分析:(解)(Ⅰ)设圆心为
 ,半径为
,半径为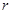 ,依题意,
,依题意,
 . ………………2分
. ………………2分设直线
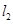 的斜率
的斜率 ,过
,过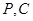 两点的直线斜率
两点的直线斜率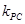 ,因
,因 ,
,故
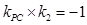 ,
,∴
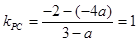 ,……4分
,……4分解得
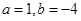 .
.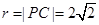 .……6分
.……6分所求圆的方程为
 .……7分
.……7分(Ⅱ)联立
 则A
则A
则
 …….……9分
…….……9分圆心
 ,
,
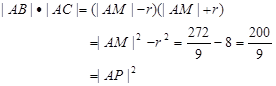 …….……13分
…….……13分所以
 得到验证 . …….………….……14分
得到验证 . …….………….……14分点评:解决该试题的关键是对于圆的方程的求解,一般采用 方法就是确定出圆心坐标,以及圆的半径即可,然后利用题目中的条件表示出求解,同时圆与直线相切的时候,切割线定理的运用也是值得关注的一点。属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
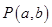 在圆C:
在圆C: 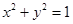 的外部,则直线
的外部,则直线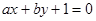 与圆C的位置关系是( )
与圆C的位置关系是( )  :
:
 为参数),圆
为参数),圆 (极轴与
(极轴与 轴的非负半轴重合,且单位长度相同)。
轴的非负半轴重合,且单位长度相同)。 到直线
到直线 ,求
,求 的值。
的值。 上的圆的方程是( )
上的圆的方程是( )



 ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点, 是
是 的中点.
的中点.
 时,求直线
时,求直线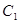 的极坐标方程是
的极坐标方程是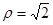 ,曲线
,曲线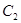 的参数方程是
的参数方程是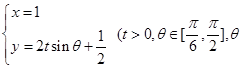 是参数).
是参数).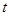 的取值范围,使得
的取值范围,使得