题目内容
已知不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,则实数a的取值范围是
- A.[-1,2]
- B.(-∞,1]
- C.(0,2]
- D.[-1,+∞)
D
分析:本题考查的是不等式与恒成立的综合类问题.在解答时,首先可以游离参数将问题转化为: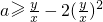 对于x∈[1,2],y∈[2,3]恒成立,然后解答此恒成立问题即可获得问题的解答.
对于x∈[1,2],y∈[2,3]恒成立,然后解答此恒成立问题即可获得问题的解答.
解答:由题意可知:不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,
即: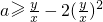 ,对于x∈[1,2],y∈[2,3]恒成立,
,对于x∈[1,2],y∈[2,3]恒成立,
令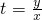 ,则1≤t≤3,
,则1≤t≤3,
∴a≥t-2t2在[1,3]上恒成立,
∵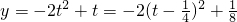
∴ymax=-1,
∴a≥-1
故选D.
点评:本题考查的是不等式与恒成立的综合类问题,综合性强,难度大,易出错.在解答的过程当中充分体现了游离参数的办法、恒成立的思想以及整体代换的技巧.值得同学们体会与反思.
分析:本题考查的是不等式与恒成立的综合类问题.在解答时,首先可以游离参数将问题转化为:
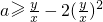 对于x∈[1,2],y∈[2,3]恒成立,然后解答此恒成立问题即可获得问题的解答.
对于x∈[1,2],y∈[2,3]恒成立,然后解答此恒成立问题即可获得问题的解答.解答:由题意可知:不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,
即:
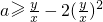 ,对于x∈[1,2],y∈[2,3]恒成立,
,对于x∈[1,2],y∈[2,3]恒成立,令
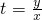 ,则1≤t≤3,
,则1≤t≤3,∴a≥t-2t2在[1,3]上恒成立,
∵
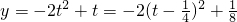
∴ymax=-1,
∴a≥-1
故选D.
点评:本题考查的是不等式与恒成立的综合类问题,综合性强,难度大,易出错.在解答的过程当中充分体现了游离参数的办法、恒成立的思想以及整体代换的技巧.值得同学们体会与反思.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目