题目内容
如图,在平面直角坐标系中,锐角 、
、 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
, 两点.
两点.

(Ⅰ)如果 ,
, 点的横坐标为
点的横坐标为 ,求
,求 的值;
的值;
(Ⅱ)若角 的终边与单位圆交于C点,设角
的终边与单位圆交于C点,设角 、
、 、
、 的正弦线分别为MA、NB、PC,求证:线段MA、NB、PC能构成一个三角形;
的正弦线分别为MA、NB、PC,求证:线段MA、NB、PC能构成一个三角形;
(III)探究第(Ⅱ)小题中的三角形的外接圆面积是否为定值?若是,求出该定值;若不是,请说明理由.
 、
、 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
, 两点.
两点.
(Ⅰ)如果
 ,
, 点的横坐标为
点的横坐标为 ,求
,求 的值;
的值;(Ⅱ)若角
 的终边与单位圆交于C点,设角
的终边与单位圆交于C点,设角 、
、 、
、 的正弦线分别为MA、NB、PC,求证:线段MA、NB、PC能构成一个三角形;
的正弦线分别为MA、NB、PC,求证:线段MA、NB、PC能构成一个三角形;(III)探究第(Ⅱ)小题中的三角形的外接圆面积是否为定值?若是,求出该定值;若不是,请说明理由.
(Ⅰ) .(Ⅱ)证明略
.(Ⅱ)证明略
(III) 的外接圆的面积为
的外接圆的面积为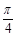 .
.
 .(Ⅱ)证明略
.(Ⅱ)证明略(III)
 的外接圆的面积为
的外接圆的面积为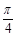 .
. (I)已知 是锐角,根据三角函数的定义,可求出
是锐角,根据三角函数的定义,可求出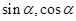 .
.
再根据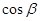 求出
求出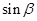 ,从而再根据两角和的余弦公式求解即可.
,从而再根据两角和的余弦公式求解即可.
(II) 依题意得,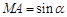 ,
,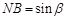 ,
,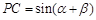 ,因为
,因为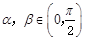 ,所以
,所以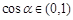 ,
,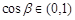 ,于是有
,于是有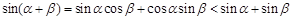 ,
,
下面解题的关键是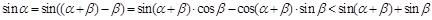 ,
,
同理,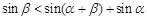 ,这样就证明三角形两边之和大于第三边,从而说明线段MA、NB、PC能构成一个三角形.
,这样就证明三角形两边之和大于第三边,从而说明线段MA、NB、PC能构成一个三角形.
(3) 不妨设 的边长分别为
的边长分别为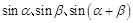 ,其中角
,其中角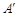 、
、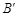 、
、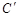 的对边分别为
的对边分别为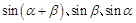 .则由余弦定理,得:
.则由余弦定理,得:
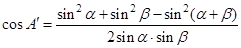 =….
=….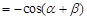 .
.
然后再利用正弦定理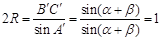 ,求出外接圆半径
,求出外接圆半径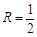 ,从而证明其外接圆面积为定值
,从而证明其外接圆面积为定值
 是锐角,根据三角函数的定义,可求出
是锐角,根据三角函数的定义,可求出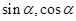 .
.再根据
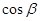 求出
求出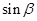 ,从而再根据两角和的余弦公式求解即可.
,从而再根据两角和的余弦公式求解即可.(II) 依题意得,
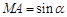 ,
,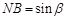 ,
,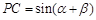 ,因为
,因为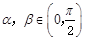 ,所以
,所以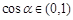 ,
,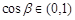 ,于是有
,于是有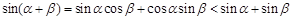 ,
,下面解题的关键是
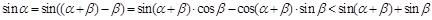 ,
,同理,
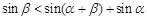 ,这样就证明三角形两边之和大于第三边,从而说明线段MA、NB、PC能构成一个三角形.
,这样就证明三角形两边之和大于第三边,从而说明线段MA、NB、PC能构成一个三角形.(3) 不妨设
 的边长分别为
的边长分别为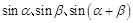 ,其中角
,其中角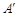 、
、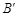 、
、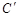 的对边分别为
的对边分别为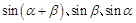 .则由余弦定理,得:
.则由余弦定理,得: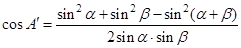 =….
=….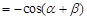 .
.然后再利用正弦定理
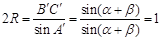 ,求出外接圆半径
,求出外接圆半径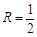 ,从而证明其外接圆面积为定值
,从而证明其外接圆面积为定值
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 ,
, ,
,  ,
, 的是( )
的是( ) 中,角A, B, C所对的边分别为a, b,c,向量
中,角A, B, C所对的边分别为a, b,c,向量 »且满足
»且满足 .
. ,求
,求 的面积.
的面积. ,则sin(α-
,则sin(α- )=_____.
)=_____.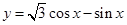 的最大值是 .
的最大值是 . 则
则 等于 .
等于 . ,
, ,则
,则 =
=