题目内容
如图,已知⊙O与CA、CB相切于点A、B,OA=OB=2 cm,AB=6 cm,则∠ACB的度数为 .
cm,AB=6 cm,则∠ACB的度数为 .
【答案】分析:过O作OD⊥AB于D;根据等腰三角形三线合一的性质知:OD垂直平分AB,且OD平分∠AOB;在Rt△OBD中,已知了OB、BD的长,可求出∠BOD的正弦值,进而可求出∠BOD、∠AOB的度数.在四边形AOBC中,∠AOB和∠ACB互补,由此可求出∠ACB的度数.
解答: 解:过O作OD⊥AB于D;
解:过O作OD⊥AB于D;
△OAB中,OA=OB,OD⊥AB;
∴AD=BD,∠AOD=∠BOD= ∠AOB(等腰三角形三线合一);
∠AOB(等腰三角形三线合一);
Rt△BOD中,OB=2 ,BD=3;
,BD=3;
∴sin∠BOD= =
= ,即∠BOD=60°;
,即∠BOD=60°;
∴∠AOB=120°;
∵CB、CA都是⊙O的切线,
∴∠OAC=∠OBC=90°;
∴∠AOB+∠ACB=180°,
∴∠ACB=180°-∠AOB=60°.
故填:60°.
点评:此题考查了垂径定理、解直角三角形、多边形的内角和、切线的性质等知识.
解答:
 解:过O作OD⊥AB于D;
解:过O作OD⊥AB于D;△OAB中,OA=OB,OD⊥AB;
∴AD=BD,∠AOD=∠BOD=
 ∠AOB(等腰三角形三线合一);
∠AOB(等腰三角形三线合一);Rt△BOD中,OB=2
 ,BD=3;
,BD=3;∴sin∠BOD=
 =
= ,即∠BOD=60°;
,即∠BOD=60°;∴∠AOB=120°;
∵CB、CA都是⊙O的切线,
∴∠OAC=∠OBC=90°;
∴∠AOB+∠ACB=180°,
∴∠ACB=180°-∠AOB=60°.
故填:60°.
点评:此题考查了垂径定理、解直角三角形、多边形的内角和、切线的性质等知识.

练习册系列答案
相关题目

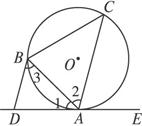
 ??
?? cm,AB=6 cm,则∠ACB的度数为 .
cm,AB=6 cm,则∠ACB的度数为 .