题目内容
已知椭圆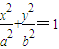 (a>b>0)的一个焦点与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,直线l:y=kx+m交椭圆于不同的两点A,B,且l总与以原点为圆心的单位圆相切.
,直线l:y=kx+m交椭圆于不同的两点A,B,且l总与以原点为圆心的单位圆相切.(I)求该椭圆的方程;
(II)当
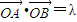 且满足
且满足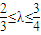 时,求S△AOB的取值范围.
时,求S△AOB的取值范围.
【答案】分析:(I)由抛物线y2=4x可知焦点为(1,0),准线为x=-1,椭圆截直线x=-1所得的弦长为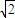 得上交点为(-1,
得上交点为(-1,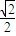 ),代入结合1=a2-b2可求
),代入结合1=a2-b2可求
II)由直线y=kx+m与圆x2+y2=1相切可得 ,由
,由 可得(1+2k2)x2+4kmx+2m2-2=0,△=8k2>0可得k≠0
可得(1+2k2)x2+4kmx+2m2-2=0,△=8k2>0可得k≠0
设A(x1,y1),B(x2,y2)则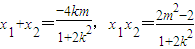 ,y1y2=(kx1+m)(kx2+m)=
,y1y2=(kx1+m)(kx2+m)=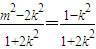 ,而
,而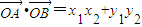 =
=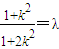 ,结合
,结合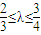 可求k的范围,根据
可求k的范围,根据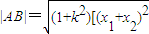 表示所求的面积,结合基本不等式可求
表示所求的面积,结合基本不等式可求
解答:解:(I)抛物线y2=4x的焦点为(1,0),准线为x=-1
∵椭圆截直线x=-1所得的弦长为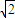 得上交点为(-1,
得上交点为(-1,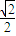 ),代入得
),代入得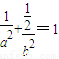 ,且1=a2-b2
,且1=a2-b2
∴b2=1,a2=2
∴椭圆方程为
(II)∵直线y=kx+m与圆x2+y2=1相切
∴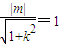 即m2=k2+1
即m2=k2+1
由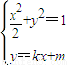 可得(1+2k2)x2+4kmx+2m2-2=0
可得(1+2k2)x2+4kmx+2m2-2=0
△=8k2>0可得k≠0
设A(x1,y1),B(x2,y2)则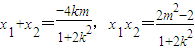
y1y2=(kx1+m)(kx2+m)=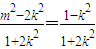
∴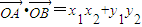 =λ,
=λ,
由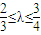 可得
可得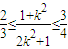 ,即
,即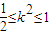
∵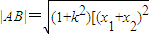 =
=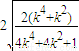
令u=k4+k2∵ ∴
∴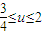 ,
,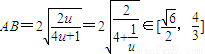
∴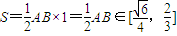
点评:本题主要考查了利用椭圆与抛物线的性质求解椭圆的方程,直线与椭圆的位置关系的应用,方程的根与系数的关系的应用及利用基本不等式求解函数的最值,综合性较强,运算量较大,属于综合试题
 得上交点为(-1,
得上交点为(-1,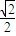 ),代入结合1=a2-b2可求
),代入结合1=a2-b2可求II)由直线y=kx+m与圆x2+y2=1相切可得
 ,由
,由 可得(1+2k2)x2+4kmx+2m2-2=0,△=8k2>0可得k≠0
可得(1+2k2)x2+4kmx+2m2-2=0,△=8k2>0可得k≠0设A(x1,y1),B(x2,y2)则
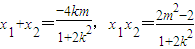 ,y1y2=(kx1+m)(kx2+m)=
,y1y2=(kx1+m)(kx2+m)=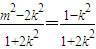 ,而
,而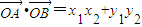 =
=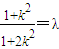 ,结合
,结合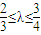 可求k的范围,根据
可求k的范围,根据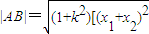 表示所求的面积,结合基本不等式可求
表示所求的面积,结合基本不等式可求解答:解:(I)抛物线y2=4x的焦点为(1,0),准线为x=-1
∵椭圆截直线x=-1所得的弦长为
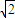 得上交点为(-1,
得上交点为(-1,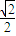 ),代入得
),代入得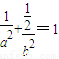 ,且1=a2-b2
,且1=a2-b2∴b2=1,a2=2
∴椭圆方程为

(II)∵直线y=kx+m与圆x2+y2=1相切
∴
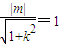 即m2=k2+1
即m2=k2+1由
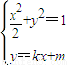 可得(1+2k2)x2+4kmx+2m2-2=0
可得(1+2k2)x2+4kmx+2m2-2=0△=8k2>0可得k≠0
设A(x1,y1),B(x2,y2)则
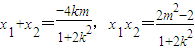
y1y2=(kx1+m)(kx2+m)=
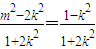
∴
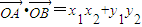 =λ,
=λ,
由
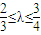 可得
可得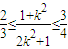 ,即
,即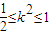
∵
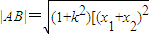 =
=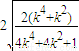
令u=k4+k2∵
 ∴
∴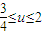 ,
,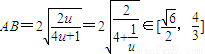
∴
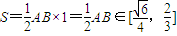
点评:本题主要考查了利用椭圆与抛物线的性质求解椭圆的方程,直线与椭圆的位置关系的应用,方程的根与系数的关系的应用及利用基本不等式求解函数的最值,综合性较强,运算量较大,属于综合试题

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.