题目内容
P:函数f(x)=sin(2x+φ)的图象关于y轴对称,Q:φ=| π | 2 |
分析:若命题P成立可求出φ的值,进而验证Q不成立;再假设Q成立时,代入到函数f(x)中,得到命题P成立,进而可知P是Q的必要不充分条件.
解答:解:若f(x)=sin(2x+φ)的图象关于y轴对称,则
f(-x)=sin[2(-x)+φ]=f(x)=sin(2x+φ)
∴sinφcos2x-cosφsin2x=sin2xcosφ+cos2xsinφ
∴sin2xcosφ=0∴cosφ=0∴φ=
+kπ,k∈Z
故由P得不到Q,故不充分;
当φ=
时,f(x)=sin(2x+
)=cos2x为偶函数,故关于y轴对称,从而Q是P的必要条件
故答案为:必要不充分.
f(-x)=sin[2(-x)+φ]=f(x)=sin(2x+φ)
∴sinφcos2x-cosφsin2x=sin2xcosφ+cos2xsinφ
∴sin2xcosφ=0∴cosφ=0∴φ=
| π |
| 2 |
故由P得不到Q,故不充分;
当φ=
| π |
| 2 |
| π |
| 2 |
故答案为:必要不充分.
点评:本题主要考查三角函数的对称性和,命题的充分必要条件.考查基础知识的综合运用能力.

练习册系列答案
相关题目
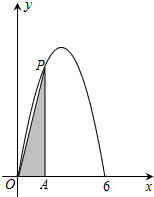 已知函数f(x)=ax2+bx+c,x∈[0,6]的图象经过(0,0)和(6,0)两点,如图所示,且函数f(x)的值域为[0,9].过动点P(t,f(t))作x轴的垂线,垂足为A,连接OP.
已知函数f(x)=ax2+bx+c,x∈[0,6]的图象经过(0,0)和(6,0)两点,如图所示,且函数f(x)的值域为[0,9].过动点P(t,f(t))作x轴的垂线,垂足为A,连接OP.