题目内容
已知离心率为
的椭圆的中心在原点，焦点在x轴上．双曲线以椭圆的长轴为实轴，短轴为虚轴，且焦距为2
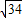．求椭圆及双曲线的方程．
【答案】分析：利用待定系数法求圆锥曲线的方程，设出椭圆方程，写出双曲线的方程；据椭圆与双曲线中的三参数的关系列出方程组，求出方程．
解答：解：设椭圆方程为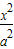
+
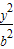=1（a＞b＞0）
则根据题意，双曲线的方程为
-
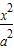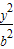=1且满足
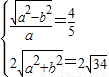解方程组得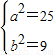
∴椭圆的方程为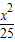
+
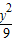=1，双曲线的方程
-
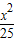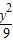=1
点评：本题考查求曲线方程常用的方法：待定系数法，使用与曲线的方程形式已知．考查椭圆中三参数的关系是：a2=b2+c2
双曲线中三参数的关系：c2=b2+a2．
解答：解：设椭圆方程为
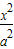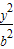+=1（a＞b＞0）则根据题意，双曲线的方程为
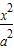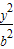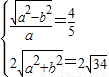-=1且满足解方程组得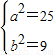∴椭圆的方程为
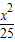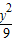+=1，双曲线的方程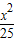-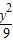=1点评：本题考查求曲线方程常用的方法：待定系数法，使用与曲线的方程形式已知．考查椭圆中三参数的关系是：a2=b2+c2
双曲线中三参数的关系：c2=b2+a2．
练习册系列答案
相关题目
. 已知离心率为
的椭圆
的右焦点
是圆
的圆心，过椭圆上的动点P作圆的两条切线分别交
轴于M、N两点．
的椭圆
上的点到
的最长距离为
，若点
在
轴上，且使得
为
的一条内角平分线，则称点
的椭圆C的中心在坐标原点O，一焦点坐标为（1，0），圆O的方程为x2+y2=7．
的椭圆
的右焦点F是圆（x-1）2+y2=1的圆心，过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点．
的椭圆
上的点到左焦点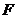
的最长距离为
，若点
在
轴上，且使得
为
的一条内角平分线，则称点