题目内容
P(x,y)是曲线
(θ为参数)上任意一点,则(x-5)2+(y+4)2的最大值为( )
|
| A.6 | B.5 | C.36 | D.25 |
由题意得:曲线
(θ为参数),消去参数θ得:
(x-2)2+y2=1表示圆心在A(2,0),半径为1的圆,
此圆上一点P(x,y)到点Q(5,-4)的距离的最大值的平方即为(x-5)2+(y+4)2的最大值,
由图得,圆上一点P(x,y)到点Q(5,-4)的距离的最大值等于:
AQ+1=
+1=5+1=6
则(x-5)2+(y+4)2的最大值为36.
故选C.
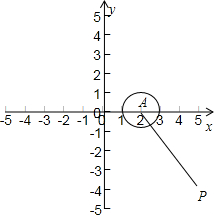
|
(x-2)2+y2=1表示圆心在A(2,0),半径为1的圆,
此圆上一点P(x,y)到点Q(5,-4)的距离的最大值的平方即为(x-5)2+(y+4)2的最大值,
由图得,圆上一点P(x,y)到点Q(5,-4)的距离的最大值等于:
AQ+1=
| (5-2)2+(-4-0)2 |
则(x-5)2+(y+4)2的最大值为36.
故选C.
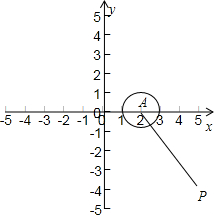

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
 的参数方程为
的参数方程为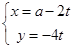 ,(
,(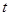 为参数),圆
为参数),圆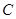 的参数方程为
的参数方程为 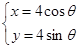 ,(
,(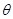 为参数).
为参数).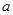 的取值范围.
的取值范围.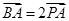 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.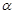 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;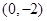 距离的最大值.
距离的最大值.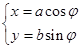
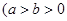 ,参数
,参数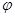 的范围是
的范围是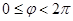 )的两个焦点为
)的两个焦点为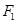 、
、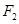 ,以
,以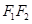 为边作正三角形,若椭圆恰好平分正三角形的另两条边,且
为边作正三角形,若椭圆恰好平分正三角形的另两条边,且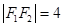 ,则
,则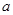 等于 .
等于 .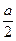 ,
,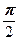 )为圆心,
)为圆心,