题目内容
不等式(x-2)2(3-x) (x-4)3(x-1)>0的解集为
{x|x<1或3<x<4}
{x|x<1或3<x<4}
.分析:利用穿根法:“奇”过“偶”不过的原理即可求得答案.
解答:解:∵(x-2)2(3-x) (x-4)3(x-1)>0,
∴(x-2)2(x-3)(x-4)3(x-1)<0,
由穿根法“奇”过“偶”不过可得:
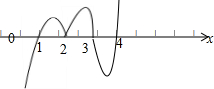
不等式(x-2)2(3-x) (x-4)3(x-1)>0的解集为{x|x<1或3<x<4}.
故答案为:{x|x<1或3<x<4}.
∴(x-2)2(x-3)(x-4)3(x-1)<0,
由穿根法“奇”过“偶”不过可得:

不等式(x-2)2(3-x) (x-4)3(x-1)>0的解集为{x|x<1或3<x<4}.
故答案为:{x|x<1或3<x<4}.
点评:本题考查高次不等式的解法,着重考查穿根法与作图能力,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目