题目内容

将(
x
+
3x
)12的展开式中各项重新排列，使含x的正整数次幂的项互不相邻的排法共有多少种？（　　）
分析：根据题意，写出(
x
+
3x
)12的展开式的通项为Tr+1=C12rx
36-5r
6
，分析可得在其展开式中，含x的正整数次幂的项共3项，不含x的正整数次幂的有10项；用插空法先将不含x的正整数次幂的10项进行全排列，可得11个空位，在其中任取3个，安排3个含x的正整数次幂的项；由分步计数原理计算可得答案．
解答：解：根据题意，(
x
+
3x
)12的展开式的通项为Tr+1=C12r（
x
）12-r（
3x
）r=C12rx
36-5r
6
，其中共13项，
若
36-5r
6
为正整数，则r的值可以为0、4、6，即其展开式中，含x的正整数次幂的项共3项，其他的有10项，
先将不含x的正整数次幂的10项进行全排列，有A1010种情况，
排好后，有11个空位，在这11个空位中，任取3个，安排3个含x的正整数次幂的项，有A113种情况，
共有A1010•A113种情况；
故选D．
点评：本题考查排列、组合的运用以及二项式定理，关键是分析出其展开式中含x的正整数次幂的项的数目，进而用插空法解题．
练习册系列答案
相关题目
下列几种说法正确的是
①③⑤
①③⑤
（将你认为正确的序号全部填在横线上）
①函数y=cos(
π
4
-3x)的递增区间是[-
π
4
+
2kπ
3
，
π
12
+
2kπ
3
]，k∈Z；
②函数f（x）=5sin（2x+?），若f（a）=5，则f(a+
π
12
)＜f(a+
5π
6
)；
③函数f(x)=3tan(2x-
π
3
)的图象关于点(
5π
12
，0)对称；
④将函数y=sin(2x+
π
3
)的图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
⑤在同一平面直角坐标系中，函数y=sin(
x
2
+
3π
2
)(x∈[0，2π])的图象和直线y=
1
2
的交点个数是1个．
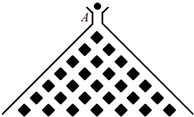（2011•丹东模拟）如图，在竖直平面内有一个“游戏滑道”，空白部分表示光滑滑道，黑色正方形表示障碍物，自上而下第一行有1个障碍物，第二行有2个障碍物，…，依此类推．一个半径适当的光滑均匀小球从入口A投入滑道，小球将自由下落，已知小球每次遇到正方形障碍物上顶点时，向左、右两边下落的概率都是
1
2
．记小球遇到第n行第m个障碍物（从左至右）上顶点的概率为P（n，m）．
（Ⅰ）求P（4，1），P（4，2）的值，并猜想P（n，m）的表达式（不必证明）；
（Ⅱ）已知f（x）=
4-x，1≤x≤3
x-3，3＜x≤6
，设小球遇到第6行第m个障碍物（从左至右）上顶点时，得到的分数为ξ=f（m），试求ξ的分布列及数学期望．
（2013•朝阳区二模）将一个质点随机投放在关于x，y的不等式组
3x+4y≤19
x≥1
y≥1
所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是
1-
π
12
1-
π
12
．
将(
x
+
3x
)12的展开式中各项重新排列，使含x的正整数次幂的项互不相邻的排法共有多少种？（　　）
A．A133•A1310B．A1010+A113C．A134•A99D．A1010•A113

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网