题目内容
设f(x)在R上可导，其导数为f′(x)，给出下列四组条件：
①p：f(x)是奇函数，q：f′(x)是偶函数；
②p：f(x)是以T为周期的函数，q：f′(x)是以T为周期的函数；
③p：f(x)在区间(－∞，＋∞)上为增函数，q：f′(x)＞0在(－∞，＋∞)恒成立；
④p：f(x)在x0处取得极值，q：f′(x0)＝0.
由以上条件中，能使p⇒q成立的序号为 ( )．
A．①②③ B．①②④ C．①③④ D．②③④
B
【解析】由f(－x)＝－f(x)，得－f′(－x)＝－f′(x)．∴f′(－x)＝f′(x)．即f′(x)是偶函数①正确．易知②正确．③不正确．根据f′(x0)＝0是可导函数f(x)在x＝x0取得极值的必要不充分条件，∴④正确．
练习册系列答案
应用题作业本系列答案
相关题目
通过随机询问110名性别不同的人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2＝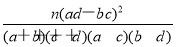
，得K2＝
≈7.8.
附表：
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论 ( )．
A．有99%以上的把握认为“选择过马路的方式与性别有关”
B．有99%以上的把握认为“选择过马路的方式与性别无关”
C．在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别有关”
D．在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别无关”