题目内容
甲乙两队参加知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
,乙队中3人答对的概率分别为
,
,
且各人正确与否相互之间没有影响.用X表示甲队的总得分.
(Ⅰ)求随机变量X分布列
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求随机变量X分布列
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
分析:(1)由题意可得X~B(3,
),利用公式P(X=i)=
(
)i(
)3-i(i=0,1,2,3)即可得到分布列.
(2)由A表示“甲、乙两个队总得分之和等于3”这一事件,B表示“甲队总得分大于乙队总得分”这一事件,可知AB表示甲对赢得3场或2场.利用相互独立事件和互斥事件的概率计算公式即可得出.
| 2 |
| 3 |
| C | i 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(2)由A表示“甲、乙两个队总得分之和等于3”这一事件,B表示“甲队总得分大于乙队总得分”这一事件,可知AB表示甲对赢得3场或2场.利用相互独立事件和互斥事件的概率计算公式即可得出.
解答:解:(1)由题意可得X~B(3,
),P(X=i)=
(
)i(
)3-i(i=0,1,2,3).
其分布列如下:
∴Eξ=3×
=2.
(2)由A表示“甲、乙两个队总得分之和等于3”这一事件,B表示“甲队总得分大于乙队总得分”这一事件,可知AB表示甲对赢得3场或2场.
∴P(AB)=(
)3×(1-
)2×(1-
)+
×(
)2×(1-
)×[
×(1-
)×(1-
)×2+(1-
)2×
]
=
.
| 2 |
| 3 |
| C | i 3 |
| 2 |
| 3 |
| 1 |
| 3 |
其分布列如下:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 3 |
(2)由A表示“甲、乙两个队总得分之和等于3”这一事件,B表示“甲队总得分大于乙队总得分”这一事件,可知AB表示甲对赢得3场或2场.
∴P(AB)=(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
=
| 34 |
| 243 |
点评:本题考查了二项分布列及其数学期望、相互独立事件和互斥事件的概率计算公式,属于难题.

练习册系列答案
相关题目
 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为 ,乙队中
,乙队中 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分. 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 。
。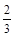 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为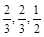 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响.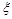 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量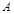 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为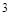 ”,用
”,用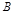 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求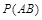 .
.