题目内容
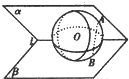 如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=
如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=| 3 |
4π
4π
.分析:设OAB平面与棱l交于点C,则△OAC为直角三角形,利用等面积,求出球的半径,从而可求球的表面积.
解答:解:设OAB平面与棱l交于点C,则△OAC为直角三角形,且AB⊥OC,OC=2

设OA=x,AC=y,则由等面积可得xy=
∵x2+y2=4
∴
或
时,∠ACO=30°,∠ACB=60°,满足题意,球的表面积为4π;
时,∠ACO=60°,∠ACB=120°,不满足题意,
故答案为:4π

设OA=x,AC=y,则由等面积可得xy=
| 3 |
∵x2+y2=4
∴
|
|
|
|
故答案为:4π
点评:本题考查球的表面积,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=
(2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB= 如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若
如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若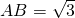 ,球心O到二面角的棱l的距离为2,则球O的表面积为________.
,球心O到二面角的棱l的距离为2,则球O的表面积为________.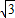 ,球心O到二面角的棱l的距离为2,则球O的表面积为( )
,球心O到二面角的棱l的距离为2,则球O的表面积为( )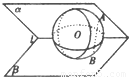
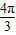
 ,球心O到二面角的棱l的距离为2,则球O的表面积为( )
,球心O到二面角的棱l的距离为2,则球O的表面积为( )
