题目内容
设函数f(x)=| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)试用a表示b;
(Ⅱ)当a=3时,求f(x)的单调区间与极值;
(Ⅲ)若a<0且f(-1)是函数f(x)的极小值,求a的取值范围.
分析:(1)函数图象过点(-1,2),将坐标代入整理可得;
(2)a=3时确定出b=-3,确定出函数解析式,求出导函数令其大于零得到增区间;令其小于零得到减区间.并求出函数的极值即可.
(3)求出导函数的极值点,因为a<0且f(-1)是函数f(x)的极小值,比较出两个驻点的大小列出不等式求出解集即可.
(2)a=3时确定出b=-3,确定出函数解析式,求出导函数令其大于零得到增区间;令其小于零得到减区间.并求出函数的极值即可.
(3)求出导函数的极值点,因为a<0且f(-1)是函数f(x)的极小值,比较出两个驻点的大小列出不等式求出解集即可.
解答:解:(Ⅰ)∵函数f(x)=
ax3+
(a+b)x2+bx的图象过点(-1,2)
∴-
a+
(a+b)-b=2,整理得,a-3b-12=0
故b=
;
(Ⅱ)当a=3时,由a-3b-12=0得,b=-3
∴f(x)=x3-3x,f′(x)=3x2-3=3(x+1)(x-1)
令f′(x)=0,解得x1=-1,x2=1.
当x变化时,f′(x),f(x)的变化情况如下表:
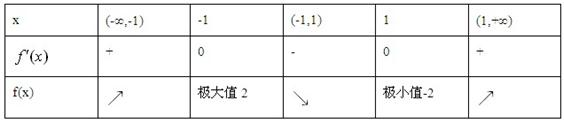
故f(x)的单调增区间是(-∞,-1),(1,+∞),单调减区间是(-1,1);极大值是f(-1)=2,极小值是f(1)=-2;
(Ⅲ)f′(x)=ax2+(a+b)x+b=(x+1)(ax+b)
∵a<0且f(-1)是函数f(x)的极小值,∴-
>-1
又∵a-3b-12=0,∴b=
,∴-
>-1
解得,a<-6
故a的取值范围为(-∞,-6).
| 1 |
| 3 |
| 1 |
| 2 |
∴-
| 1 |
| 3 |
| 1 |
| 2 |
故b=
| a-12 |
| 3 |
(Ⅱ)当a=3时,由a-3b-12=0得,b=-3
∴f(x)=x3-3x,f′(x)=3x2-3=3(x+1)(x-1)
令f′(x)=0,解得x1=-1,x2=1.
当x变化时,f′(x),f(x)的变化情况如下表:

故f(x)的单调增区间是(-∞,-1),(1,+∞),单调减区间是(-1,1);极大值是f(-1)=2,极小值是f(1)=-2;
(Ⅲ)f′(x)=ax2+(a+b)x+b=(x+1)(ax+b)
∵a<0且f(-1)是函数f(x)的极小值,∴-
| b |
| a |
又∵a-3b-12=0,∴b=
| a-12 |
| 3 |
| a-12 |
| 3a |
解得,a<-6
故a的取值范围为(-∞,-6).
点评:考查学生利用导数研究函数的单调性的能力即利用导数研究函数极值的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目