题目内容
已知数列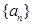 的前
的前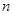 项和为
项和为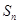 ,点
,点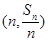 在直线
在直线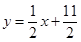 上.数列
上.数列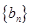 满足
满足
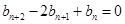
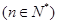 ,
,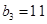 ,且其前9项和为153.
,且其前9项和为153.
(Ⅰ)求数列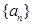 ,
,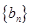 的通项公式;
的通项公式;
(Ⅱ)设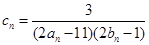 ,数列
,数列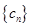 的前
的前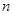 项和为
项和为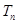 ,求使不等式
,求使不等式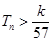 对一切
对一切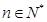 都成立的最大正整数
都成立的最大正整数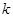 的值.
的值.
解:(Ⅰ)由已知得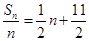 ,
,
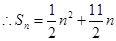 …………1分
…………1分
当 时,
时,
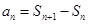
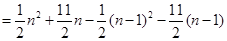
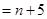 …………3分
…………3分
当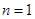 时,
时,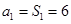 也符合上式. (没有检验
也符合上式. (没有检验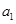 扣1分)
扣1分)
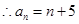 ,
, 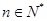 .
…………4分
.
…………4分
由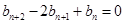
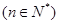 知
知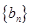 是等差数列,
…………5分
是等差数列,
…………5分
由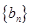 的前9项和为153,可得
的前9项和为153,可得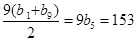 ,
,
得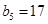 ,又
,又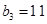 ,
,
∴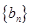 的公差
的公差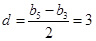 ,
,
由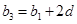 ,得
,得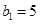 ,
,
∴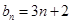 ,
, 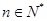 .
…………7分
.
…………7分
(Ⅱ)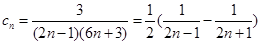 ,
…………9分
,
…………9分
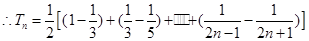
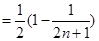 …………10分
…………10分
∵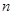 增大,
增大,
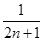 减小
,
减小
, 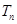 增大,
增大,
∴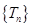 是递增数列.
是递增数列.
∴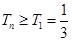 .
即
.
即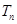 的最小值为
的最小值为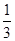 …………12分
…………12分
要使得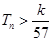 对一切
对一切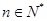 都成立,只要
都成立,只要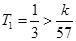 ,
,
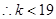 ,则
,则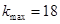 .
…………14分
.
…………14分
【解析】本试题主要是考查了数列的通项公式的求解和求和的运用。
(1))由已知得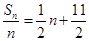 ,利用前n项和与通项公式的关系得到通项公式的结论。
,利用前n项和与通项公式的关系得到通项公式的结论。
(2)因为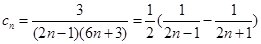 ,利用裂项求和得到结论。,并证明不等式。
,利用裂项求和得到结论。,并证明不等式。

 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式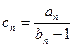 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.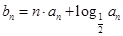 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.