题目内容
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2•a6
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)设bn=log3a1+log3a2+…+log3an,记数列{
}的前n项和为Tn.若对于?n∈N*,恒有Tn>
成立,其中m∈N*,求m的最小值.
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)设bn=log3a1+log3a2+…+log3an,记数列{
| 1 |
| bn |
| 1-m |
| 1005 |
分析:(1)设等比数列{an}的公比为q,依题意,列出关于首项a1与公比q的方程组,解之即可求得数列{an}的通项公式;
(2)按照比数列{an}的前n项和公式求之即可;
(3)求得数列{
}的前n项和为Tn,对于?n∈N*,恒有Tn>
成立,其中m∈N*,即可求得m的最小值.
(2)按照比数列{an}的前n项和公式求之即可;
(3)求得数列{
| 1 |
| bn |
| 1-m |
| 1005 |
解答:解:(1)设等比数列{an}的公比为q,则
,解得a1=
,q=
,
∴an=
;
(2)∴数列{an}的前n项和Sn=
=
(1-
);
(3)∵bn=log3a1+log3a2+…+log3an=-1-2-…-n=-
,
∴
=-
=-2(
-
),
∴Tn=-2[(1-
)+(
-
)+…+(
-
)]
=-2(1-
)=-
.
∵Tn>
恒成立,
即-
>
恒成立,又m∈N*,
∴m>2011-
恒成立,
∴mmin=2011.
|
| 1 |
| 3 |
| 1 |
| 3 |
∴an=
| 1 |
| 3n |
(2)∴数列{an}的前n项和Sn=
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 3n |
(3)∵bn=log3a1+log3a2+…+log3an=-1-2-…-n=-
| n(n+1) |
| 2 |
∴
| 1 |
| bn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=-2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=-2(1-
| 1 |
| n+1 |
| 2n |
| n+1 |
∵Tn>
| 1-m |
| 1005 |
即-
| 2n |
| n+1 |
| 1-m |
| 1005 |
∴m>2011-
| 2 |
| n+1 |
∴mmin=2011.
点评:本题考查数列的求和,考查等比数列的通项公式与求和公式的综合应用,属于中档题.

练习册系列答案
相关题目
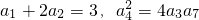 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .