题目内容
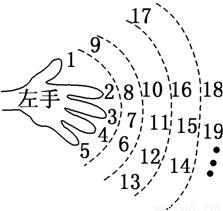
“欢欢”按如图所示的规则练习数数,记在数数过程中对应中指的数依次排列所构成的数列为{an},则数到2 008时对应的指头是 ,数列{an}的通项公式an= .(填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).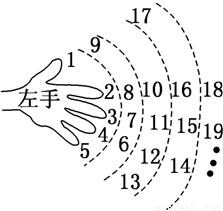
【答案】分析:注意到数1,9,17,25,,分别都对应着大拇指,且1+8×(251-1)=2001,因此数到2008时对应的指头是食指.对应中指的数依次是:3,7,11,15,,因此数列{an}是3为首项4为公差的等差数列,根据等差数列的通项公式即可得到答案.
解答:解:∵数1,9,17,25,,分别都对应着大拇指,且1+8×(251-1)=2001,
∴数到2008时对应的指头是食指.
∵对应中指的数依次是:3,7,11,15,因此数列{an}的通项公式是an=3+(n-1)×4=4n-1.
故答案为:食指,4n-1
点评:本题主要考查等差数列的性质,注意等差数列的确定.
解答:解:∵数1,9,17,25,,分别都对应着大拇指,且1+8×(251-1)=2001,
∴数到2008时对应的指头是食指.
∵对应中指的数依次是:3,7,11,15,因此数列{an}的通项公式是an=3+(n-1)×4=4n-1.
故答案为:食指,4n-1
点评:本题主要考查等差数列的性质,注意等差数列的确定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
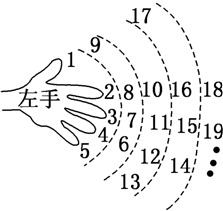 15、“欢欢”按如图所示的规则练习数数,记在数数过程中对应中指的数依次排列所构成的数列为{an},则数到2 008时对应的指头是
15、“欢欢”按如图所示的规则练习数数,记在数数过程中对应中指的数依次排列所构成的数列为{an},则数到2 008时对应的指头是