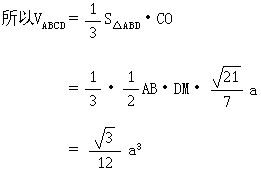Question

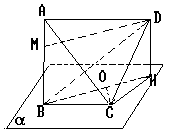
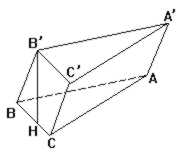
判断正误：

如图, 已知B、C∈α, AB⊥α于B, CD与α成30°角, ∠BCD ＝ 90°, 若AB ＝ BC ＝ CD ＝a

则AD的长是a

(    )

四面体ABCD的体积是a3

(    )

Answer 1

答案：F;F
解析：

解: 过D作DH⊥α于H, 则∠DCH＝30°, 所以DH＝ 因为AB⊥α,  所以DH∥AB,过D作DM⊥AB于M, 则DM＝BH,且DM∥BH， 所以DH＝BM＝AM＝ 又 因为BC＝CD＝a,∠BCD＝90°, 所以BD＝a,  因为AD＝a,  因为AB⊥α, 所以面ABHD⊥α, 过C作CO⊥BH于O, 则CO⊥面ABD, 因为∠BCD＝90°, ∠BCH＝90°, CH＝a, 所以BH＝a,CO＝＝a

提示：

①过D作DH⊥α ，DH与BA可确定一个平面. ∠DCH＝30° ②过D作DM⊥AB于M， DM∥BH ③在α内作CO⊥BH于O ④VABCD＝S△ABD·CO.