题目内容
（本小题满分12分）
已知双曲线的渐近线方程为y＝±x，并且焦点都在圆x2＋y2＝100上，求双曲线方程．
【答案】
所求双曲线方程为－＝1或－＝1
【解析】解：（1）当焦点在x轴上时，设双曲线方程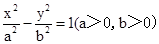
由渐近线方程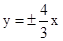
得
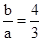，①
又焦点在圆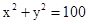
上，知c=10，
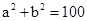②
由①②解得a=6，b=8
∴所求双曲线方程为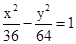
(2)当焦点在y轴上时，设双曲线方程为－＝1(a>0，b>0)，
则⇒
∴所求双曲线方程为－＝1.
综上，所求双曲线方程为－＝1或－＝1.
练习册系列答案
口算题天天练系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
