题目内容
已知函数f(x)=(x-2)2,f′(x)是函数f(x)的导函数,设a1=3,an+1=an-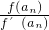
(I)证明:数列{an-2}是等比数列,并求出数列{an}的通项公式;
(II)令bn=nan,求数列{bn}的前n项和Sn.
解:(I)f′(x)=2(x-2),由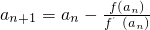 ,
,
可得 ,
,
 ,
,
∴{an-2}是以a1-2=1为首项,公比为 的等比数列,
的等比数列,
∴ ,
,
∴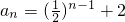 .
.
(Ⅱ)由题意 ,
,
则 (9分)
(9分)
令 ①
①
①× 得:
得: ②
②
①-②得:
= =2(1-
=2(1- )-
)- ,
,
即 (12分)
(12分)
所以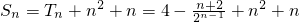 (13分)
(13分)
分析:(I)f′(x)=2(x-2),由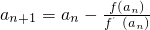 ,可得
,可得 ,
, ,由此能够证明数列{an-2}是等比数列,并能求出数列{an}的通项公式.
,由此能够证明数列{an-2}是等比数列,并能求出数列{an}的通项公式.
(Ⅱ)由题意 ,则
,则 ,令
,令 ,由错位相减法能够求出
,由错位相减法能够求出 ,所以
,所以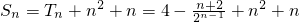 .
.
点评:第(I)题考查等比数列的证明和通项公式的求法,解题时要注意合理地构造数列;第(II)题考查数列前n项和的求法,解题时要注意错位相减法的合理运用.
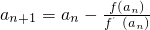 ,
,可得
 ,
, ,
,∴{an-2}是以a1-2=1为首项,公比为
 的等比数列,
的等比数列,∴
 ,
,∴
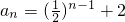 .
.(Ⅱ)由题意
 ,
,则
 (9分)
(9分)令
 ①
①①×
 得:
得: ②
②①-②得:

=
 =2(1-
=2(1- )-
)- ,
,即
 (12分)
(12分)所以
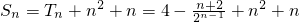 (13分)
(13分)分析:(I)f′(x)=2(x-2),由
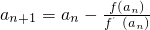 ,可得
,可得 ,
, ,由此能够证明数列{an-2}是等比数列,并能求出数列{an}的通项公式.
,由此能够证明数列{an-2}是等比数列,并能求出数列{an}的通项公式.(Ⅱ)由题意
 ,则
,则 ,令
,令 ,由错位相减法能够求出
,由错位相减法能够求出 ,所以
,所以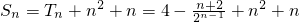 .
.点评:第(I)题考查等比数列的证明和通项公式的求法,解题时要注意合理地构造数列;第(II)题考查数列前n项和的求法,解题时要注意错位相减法的合理运用.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|