题目内容
()(本小题满分13分)
设椭圆![]() 过点
过点![]() ,且着焦点为
,且着焦点为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交与两不同点
相交与两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足![]() ,证明:点
,证明:点![]() 总在某定直线上
总在某定直线上
(Ⅰ)![]()
(Ⅱ)见解析
解析:
(1)由题意:
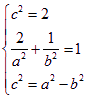 ,解得
,解得![]() ,所求椭圆方程为
,所求椭圆方程为 ![]()
(2)方法一
设点Q、A、B的坐标分别为![]() 。
。
由题设知![]() 均不为零,记
均不为零,记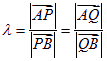 ,则
,则![]() 且
且![]()
又A,P,B,Q四点共线,从而![]()
于是 ![]() ,
, ![]()
![]() ,
, ![]()
从而
![]() ,
,![]() (1)
(1) ![]() ,
,![]() (2)
(2)
又点A、B在椭圆C上,即
![]()
![]()
(1)+(2)×2并结合(3),(4)得![]()
即点![]() 总在定直线
总在定直线![]() 上
上
方法二
设点![]() ,由题设,
,由题设,![]() 均不为零。
均不为零。
且 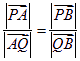
又 ![]() 四点共线,可设
四点共线,可设![]() ,于是
,于是
![]() (1)
(1)
![]() (2)
(2)
由于![]() 在椭圆C上,将(1),(2)分别代入C的方程
在椭圆C上,将(1),(2)分别代入C的方程![]() 整理得
整理得
![]() (3)
(3)
![]() (4)
(4)
(4)-(3) 得 ![]()
![]()
即点![]() 总在定直线
总在定直线![]() 上
上

练习册系列答案
相关题目
(本小题满分13分)
随机变量X的分布列如下表如示,若数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
, ).现随机变量X∽Q(
).现随机变量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求随机变量X的数学期望EX;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
 经过点
经过点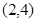 .
.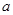 的值;(2)求
的值;(2)求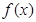 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.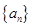 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,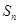 为
为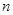 项和.
项和.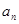 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列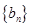 的通项公式及其前
的通项公式及其前 .
.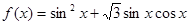

 的最小正周期和值域;
的最小正周期和值域; 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图
象,求函数
的图
象,求函数 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出

