题目内容
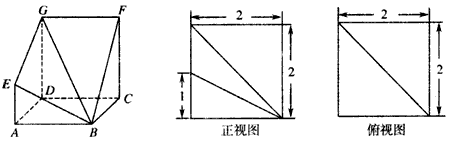
如图,多面体ABCDEFG中,面ABCD为正方形,AE,BF,DG均垂直于平面ABCD,且AB=AE=4,BF=DG=2,M,N分别为AB,BC的中点.(1)若P为BF的中点,证明NP∥平面EGM;
(2)求三棱锥N-EGM体积.

【答案】分析:(1)取AE的中点H,根据面BCF∥面ADGE推出PN∥EG,根据直线与平面的性质定理可知PN∥面EGM;
(2)将三棱锥N-EGM体积转化成VN-EGM=VP-EGM=VG-EMP=VD-EMP,又AD⊥面ABEF,DC∥AE,再根据三棱锥的体积公式进行求解即可.
解答:解:(1)取AE的中点H,由题意知,BF∥AE,BC∥AD
∴面BCF∥面ADGE,
∴FC∥HD∥EG,又PN∥FC,
∴PN∥EG.
∴PN∥面EGM
(2)∵PN∥面EGM,
∴VN-EGM=VP-EGM=VG-EMP=VD-EMP,
又AD⊥面ABEF,DC⊥AE,
∴ .
.
点评:本题主要考查了直线与平面平行的判定,以及三棱锥的体积的公式,属于基础题.
(2)将三棱锥N-EGM体积转化成VN-EGM=VP-EGM=VG-EMP=VD-EMP,又AD⊥面ABEF,DC∥AE,再根据三棱锥的体积公式进行求解即可.
解答:解:(1)取AE的中点H,由题意知,BF∥AE,BC∥AD
∴面BCF∥面ADGE,
∴FC∥HD∥EG,又PN∥FC,
∴PN∥EG.
∴PN∥面EGM
(2)∵PN∥面EGM,
∴VN-EGM=VP-EGM=VG-EMP=VD-EMP,
又AD⊥面ABEF,DC⊥AE,
∴
 .
.点评:本题主要考查了直线与平面平行的判定,以及三棱锥的体积的公式,属于基础题.

练习册系列答案
相关题目


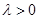 使得
使得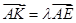 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为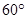 ,求
,求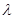 的值。
的值。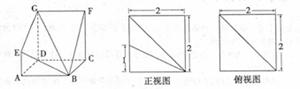
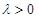 使得
使得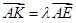 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为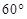 ,求
,求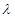 的值。
的值。
 使得
使得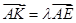 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为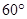 ,求
,求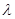 的值。
的值。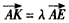 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。