题目内容
在△ABC中,给出下列4个式子:①sin(A+B)+sinC;②cos(A+B)+cosC;③sin(
A.①② B.②③ C.③④ D.①④
解析:对于②,cos(A+B)+cosC=cos(180°-C)+cosC=-cosC+cosC=0;
对于③,sin(
=sin(360°
答案:B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为
| 条 件 | 方 程 | ||||
| ①△ABC的周长为10 | C1:y2=25 | ||||
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) | ||||
| ③△ABC中,∠A=90° | C3:
|
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
| A、C3、C1、C2 |
| B、C2、C1、C3 |
| C、C1、C3、C2 |
| D、C3、C2、C1 |
在△ABC中,A(x,y),B(-2,0),C(2,0),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别用代号表示为( )
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
| 条件 | 方程 |
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° | E1:y2=25; E2:x2+y2=4(y≠0); E3: 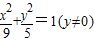 |
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
| 条 件 | 方 程 |
| ①△ABC的周长为10 | C1:y2=25 |
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3: |