题目内容
已知正方体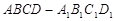 的棱长为
的棱长为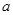 .
.
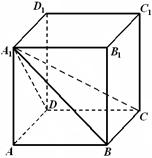
(1)求异面直线 与
与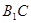 所成角的大小;
所成角的大小;
(2)求四棱锥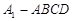 的体积.
的体积.
【答案】
(1)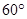 ;(2)
;(2)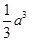 .
.
【解析】
试题分析:这是最基本的立体几何题,计算异面直线所成的角和几何体的体积.(1)异面直线直线所成的角,主要是根据定义把两条异面直线中的一条平移到与另一条相交,则这两条相交直线所成的锐角或直角就是所求,正方体中平行线很多,不需要另外作辅助线,如 ∥
∥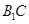 ,则
,则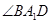 (或其补角)就是所求异面直线所成的角.(2)这是求一个四棱锥的体积,为底面积乘高除以3,本题中四棱锥底面是正方形
(或其补角)就是所求异面直线所成的角.(2)这是求一个四棱锥的体积,为底面积乘高除以3,本题中四棱锥底面是正方形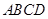 ,高是
,高是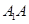 ,体积易求.
,体积易求.
试题解析:(1)因为
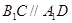 ,
,
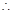 直线
直线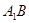 与
与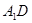 所成的角就是异面直线
所成的角就是异面直线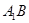 与
与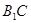 所成角.
所成角.
又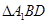 为等边三角形,
为等边三角形,
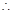 异面直线
异面直线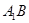 与
与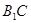 所成角的大小为
所成角的大小为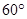 .
.
(2)四棱锥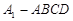 的体积
的体积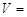
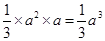
考点:(1)异面直线所成的角;(2)棱锥的体积.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知正方体的棱长为2,则其外接球的半径为( )
| A、2 | ||
B、2
| ||
C、2
| ||
D、
|
已知正方体的棱长为1,则该正方体外接球的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|