��Ŀ����
��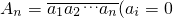 ��1��i=1��2������n�������AnΪ0��1��һ��nλ���У�����An��������
��1��i=1��2������n�������AnΪ0��1��һ��nλ���У�����An��������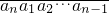 ��ΪR1��An����������
��ΪR1��An����������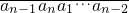 ��ΪR2��An�����������ƣ�ֱ��Rn��An��=An����������An��Ri��An����i=1��2������n-1�������Ƕ�Ӧλ��������ͬ�ĸ�����ȥ��Ӧλ�����ֲ�ͬ�ĸ���������An��Ri��An�������ֵ������
��ΪR2��An�����������ƣ�ֱ��Rn��An��=An����������An��Ri��An����i=1��2������n-1�������Ƕ�Ӧλ��������ͬ�ĸ�����ȥ��Ӧλ�����ֲ�ͬ�ĸ���������An��Ri��An�������ֵ������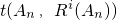 ������
������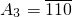 ����
����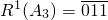 ��
��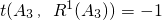 ����
����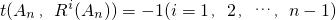 �����AnΪ������У�
�����AnΪ������У�
���������������A3��
����֤�����������������A5��
������ij��A2k+1��k����������Ϊ������У�������A2k+1��1�ĸ�����
���⣺�������A3Ϊ 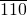 ��
��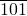 ��
��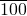 ��
�� ��
��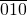 ��
�� �� ����3�֣�
�� ����3�֣�
����֤������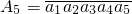 ����
����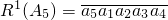 ��
��
��Ϊ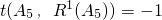 ������|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1��
������|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1��
��a5��a1��a2��a3��a4��a5��˳���о�����仯��������������֪��2�����벻�����ı䣬��3�����뷢���˸ı䣮
����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��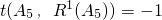 ��
��
�Ӷ��������������A5�� ����7�֣�
���⣺��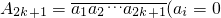 ��1��i=1��2������2k+1������
��1��i=1��2������2k+1������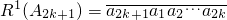 ��
��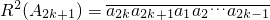 ��
��
��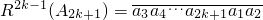 ��
�� ��
��
��Ϊ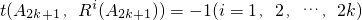 ��
��
���� A2k+1��ÿ��Ri��A2k+1����k����Ӧλ��������ͬ����k+1����Ӧλ�����벻ͬ��
�����|a1-a2k+1|+|a2-a1|+��+|a2k-a2k-1|+|a2k+1-a2k|=k+1��|a1-a2k|+|a2-a2k+1|+��+|a2k-a2k-2|+|a2k+1-a2k-1|=k+1��
����|a1-a3|+|a2-a4|+��+|a2k-a1|+|a2k+1-a2|=k+1��|a1-a2|+|a2-a3|+��+|a2k-a2k+1|+|a2k+1-a1|=k+1��
���ϸ�ʽ��͵ã�S=��k+1����2k�� ����10�֣�
��һ���棬S������������ͣ���a1��a2������a2k��a2k+1����x��0��y��1����S=2xy������11�֣�
����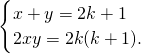 ���
���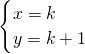 ��
��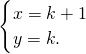 ��
��
��������A2k+1��1�ĸ�����k��k+1�� ����13�֣�
������������������еĶ���ɵã��������A3Ϊ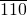 ��
��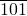 ��
��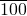 ��
�� ��
��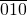 ��
�� ��
��
������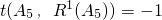 ���ɵ�|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��
���ɵ�|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��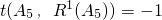 ��
��
���� A2k+1��ÿ��Ri��A2k+1����k����Ӧλ��������ͬ����k+1����Ӧλ�����벻ͬ����a1��a2������a2k��a2k+1����x��0��y��1����S=2xy���ɵ�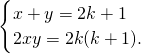 �����
�����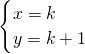 ��
��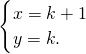 ���Ӷ��ó����ۣ�
���Ӷ��ó����ۣ�
������������Ҫ�������С�����Լ�����ԭ����Ӧ�ã������˷������۵���ѧ˼�룬�������⣮
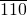 ��
��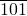 ��
��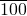 ��
�� ��
��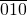 ��
�� �� ����3�֣�
�� ����3�֣�����֤������
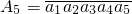 ����
����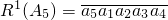 ��
����Ϊ
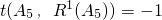 ������|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1��
������|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1����a5��a1��a2��a3��a4��a5��˳���о�����仯��������������֪��2�����벻�����ı䣬��3�����뷢���˸ı䣮
����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��
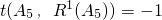 ��
���Ӷ��������������A5�� ����7�֣�
���⣺��
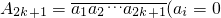 ��1��i=1��2������2k+1������
��1��i=1��2������2k+1������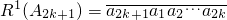 ��
��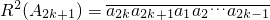 ��
����
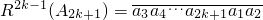 ��
�� ��
����Ϊ
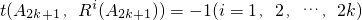 ��
������ A2k+1��ÿ��Ri��A2k+1����k����Ӧλ��������ͬ����k+1����Ӧλ�����벻ͬ��
�����|a1-a2k+1|+|a2-a1|+��+|a2k-a2k-1|+|a2k+1-a2k|=k+1��|a1-a2k|+|a2-a2k+1|+��+|a2k-a2k-2|+|a2k+1-a2k-1|=k+1��
����|a1-a3|+|a2-a4|+��+|a2k-a1|+|a2k+1-a2|=k+1��|a1-a2|+|a2-a3|+��+|a2k-a2k+1|+|a2k+1-a1|=k+1��
���ϸ�ʽ��͵ã�S=��k+1����2k�� ����10�֣�
��һ���棬S������������ͣ���a1��a2������a2k��a2k+1����x��0��y��1����S=2xy������11�֣�
����
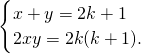 ���
���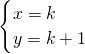 ��
��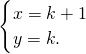 ��
����������A2k+1��1�ĸ�����k��k+1�� ����13�֣�
������������������еĶ���ɵã��������A3Ϊ
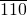 ��
��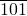 ��
��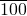 ��
�� ��
��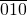 ��
�� ��
�� ������
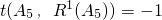 ���ɵ�|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��
���ɵ�|a1-a5|��|a2-a1|��|a3-a2|��|a4-a3|��|a5-a4|֮����2��0��3��1����a5��������������ı䲻�ܻص����������Բ�����A5��ʹ��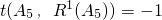 ��
������ A2k+1��ÿ��Ri��A2k+1����k����Ӧλ��������ͬ����k+1����Ӧλ�����벻ͬ����a1��a2������a2k��a2k+1����x��0��y��1����S=2xy���ɵ�
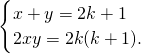 �����
�����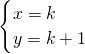 ��
��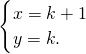 ���Ӷ��ó����ۣ�
���Ӷ��ó����ۣ�������������Ҫ�������С�����Լ�����ԭ����Ӧ�ã������˷������۵���ѧ˼�룬�������⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
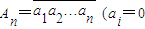 ��1��i=1��2������n�������AnΪ0��1��һ��nλ���У�����An��������
��1��i=1��2������n�������AnΪ0��1��һ��nλ���У�����An��������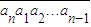 ��ΪR1��An����������
��ΪR1��An����������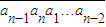 ��ΪR2��An�����������ƣ�ֱ��Rn��An��=An����������An��Ri��An����i=1��2������n-1�������Ƕ�Ӧλ��������ͬ�ĸ�����ȥ��Ӧλ�����ֲ�ͬ�ĸ���������An��Ri��An�������ֵ������
��ΪR2��An�����������ƣ�ֱ��Rn��An��=An����������An��Ri��An����i=1��2������n-1�������Ƕ�Ӧλ��������ͬ�ĸ�����ȥ��Ӧλ�����ֲ�ͬ�ĸ���������An��Ri��An�������ֵ������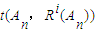 ������
������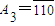 ����
����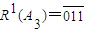 ��
��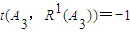 ����
����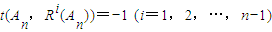 �����AnΪ������У�
�����AnΪ������У�