题目内容
选修4-2:矩阵及其变换(1)如图,向量
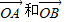 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
,(Ⅰ)求矩阵M;
(Ⅱ)并求
 在M作用后的函数解析式;
在M作用后的函数解析式;选修4-4:坐标系与参数方程
( 2)在直角坐标系x0y中,直线l的参数方程为
 (t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
.(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B.若点P的坐标为(3,
 ),求|PA|+|PB|.
),求|PA|+|PB|.选修4-5:不等式选讲
(3)已知x,y,z为正实数,且
 ,求x+4y+9z的最小值及取得最小值时x,y,z的值.
,求x+4y+9z的最小值及取得最小值时x,y,z的值.
【答案】分析:(1)(Ⅰ)二阶矩阵把点变换成点,利用待定系数法及二阶矩阵与平面列向量的乘法,可求矩阵M,
(Ⅱ)二阶矩阵把点变换成点,借此又可解决坐标变换问题,注意变换前后点的坐标间的关系.
(2)(Ⅰ)由圆C的方程为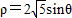 ,能求出圆的直角方程.
,能求出圆的直角方程.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得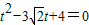 ,再由点P的坐标为(3,
,再由点P的坐标为(3,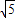 ),能求出|PA|+|PB|.
),能求出|PA|+|PB|.
(3)由柯西不等式,得x+4y+9z=[( )2+(2
)2+(2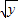 )2+(3
)2+(3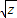 )2]•[(
)2]•[(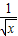 )2+(
)2+(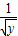 )2+(
)2+(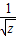 )2],由此能求出x+4y+9z取得最小值.
)2],由此能求出x+4y+9z取得最小值.
解答:解:(1)(Ⅰ)设M=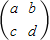 ,
,
∵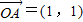 ,
,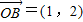 矩阵M作用后分别变成
矩阵M作用后分别变成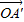 =(2,2),
=(2,2),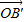 =(2,4),
=(2,4),
∴用待定系数求得M=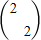 .(4分)
.(4分)
(Ⅱ)∵M=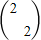 ,∴
,∴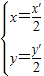 ,解得
,解得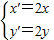 ,
,
再坐标转移法得y′=2sin(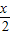 +
+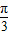 ).(7分)
).(7分)
(2)(Ⅰ)∵圆C的方程为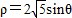 ,
,
∴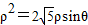 ,
,
∴圆的直角方程: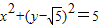
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得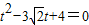
由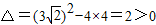 ,故可设t1,t2是上述方程的两根
,故可设t1,t2是上述方程的两根
所以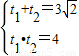 ,又直线l过点
,又直线l过点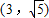 ,故结合t的几何意义得
,故结合t的几何意义得
|PA|+|PB|=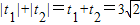 .…7 分
.…7 分
(3)解:由柯西不等式得
x+4y+9z=[(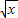 )2+(2
)2+(2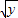 )2+(3
)2+(3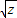 )2]•[(
)2]•[(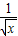 )2+(
)2+(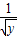 )2+(
)2+(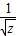 )2]
)2]
≥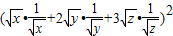
=36.…(4分)
当且仅当x=2y=3z时等号成立,…(5分)
此时x=6,y=3,z=2…(6分)
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.…(7分)
点评:第(1)题考查矩阵及其变换,第(2)题考查坐标第与参数方程,第(3)题考查不等式.这三道小题都是基础题,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
(Ⅱ)二阶矩阵把点变换成点,借此又可解决坐标变换问题,注意变换前后点的坐标间的关系.
(2)(Ⅰ)由圆C的方程为
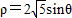 ,能求出圆的直角方程.
,能求出圆的直角方程.(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得
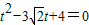 ,再由点P的坐标为(3,
,再由点P的坐标为(3,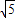 ),能求出|PA|+|PB|.
),能求出|PA|+|PB|.(3)由柯西不等式,得x+4y+9z=[(
 )2+(2
)2+(2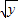 )2+(3
)2+(3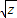 )2]•[(
)2]•[(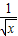 )2+(
)2+(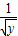 )2+(
)2+(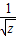 )2],由此能求出x+4y+9z取得最小值.
)2],由此能求出x+4y+9z取得最小值.解答:解:(1)(Ⅰ)设M=
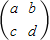 ,
,∵
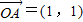 ,
,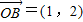 矩阵M作用后分别变成
矩阵M作用后分别变成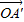 =(2,2),
=(2,2),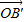 =(2,4),
=(2,4),∴用待定系数求得M=
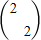 .(4分)
.(4分)(Ⅱ)∵M=
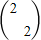 ,∴
,∴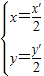 ,解得
,解得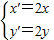 ,
,再坐标转移法得y′=2sin(
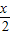 +
+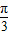 ).(7分)
).(7分)(2)(Ⅰ)∵圆C的方程为
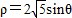 ,
,∴
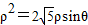 ,
,∴圆的直角方程:
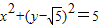
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得
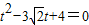
由
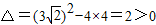 ,故可设t1,t2是上述方程的两根
,故可设t1,t2是上述方程的两根所以
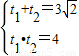 ,又直线l过点
,又直线l过点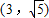 ,故结合t的几何意义得
,故结合t的几何意义得|PA|+|PB|=
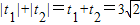 .…7 分
.…7 分(3)解:由柯西不等式得
x+4y+9z=[(
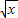 )2+(2
)2+(2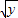 )2+(3
)2+(3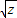 )2]•[(
)2]•[(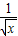 )2+(
)2+(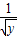 )2+(
)2+(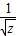 )2]
)2]≥
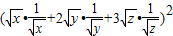
=36.…(4分)
当且仅当x=2y=3z时等号成立,…(5分)
此时x=6,y=3,z=2…(6分)
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.…(7分)
点评:第(1)题考查矩阵及其变换,第(2)题考查坐标第与参数方程,第(3)题考查不等式.这三道小题都是基础题,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 选修4-2:矩阵及其变换
选修4-2:矩阵及其变换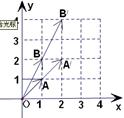
 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
,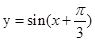 在M作用后的函数解析式;
在M作用后的函数解析式;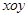 中,直线
中,直线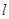 的参数方程为
的参数方程为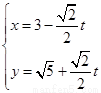 (
(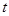 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系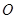 为极点,以
为极点,以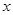 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为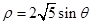 。
。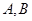 。若点
。若点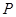 的坐标为(3,
的坐标为(3,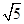 ),求
),求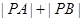 。
。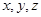 为正实数,且
为正实数,且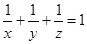 ,求
,求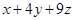 的最小值及取得最小值时
的最小值及取得最小值时 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
, 在M作用后的函数解析式;
在M作用后的函数解析式; (t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系x0y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ),求|PA|+|PB|.
),求|PA|+|PB|. ,求x+4y+9z的最小值及取得最小值时x,y,z的值.
,求x+4y+9z的最小值及取得最小值时x,y,z的值.