题目内容
已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.(文科):
(1)求异面直线B1A与直线C1D所成角大小;
(2)求二面角A1-CD-A的大小;
(理科):
(1)求异面直线B1D与直线AC所成角大小;
(2)求点C到平面B1C1D的距离.

【答案】分析:(文科)(1)本题图形中出现了同一点出发的三条两两垂直的线段,故可以建立空间坐标系用向量法求解,写出要用的点的坐标,得到对应的异面直线的方向向量,根据向量所成的角得到结果.
(2)设出一个平面的法向量,根据向量垂直的条件,得到法向量的坐标之间的关系,写出其中一个,另一个平面上的法向量可以看出法向量,根据两个向量所成的角得到二面角.
(理科)(1)本题图形中出现了同一点出发的三条两两垂直的线段,故可以建立空间坐标系用向量法求解,写出要用的点的坐标,得到对应的异面直线的方向向量,根据向量所成的角得到结果.
(2)根据三棱锥D-B1C1C的体积易得,故可用等体积法求解,由于VD-B1C1C=VC-B1C1D,点D到面B1C1C的距离是2,三角形B1C1C的面积是4,又点D到线B1C1的距离为2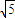 ,故三角形DB1C1的面积可得,代入求出点到面的距离
,故三角形DB1C1的面积可得,代入求出点到面的距离
解答: 解:直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,故可解得此棱柱的高是4
解:直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,故可解得此棱柱的高是4
如图,以AB所在直线为X轴,以AD所在直线为Y轴,以AA1所在直线为Z轴建立空间坐标系,由上知A(0,0,0),B(2,0,0),C(2,2,0),D(0,6,0),A1(0,0,4),B1(2,0,4),C1(2,2,4),D1(0,6,4)
(文科):
(1)由题意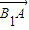 =(-2,0,-4),
=(-2,0,-4),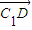 =(-2,4,-4)
=(-2,4,-4)
两向量夹角的余弦值为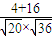 =
=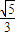
故两直线所成的角为arccos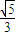
(2)由于面ACD是坐标平面,故其法向量可设为(0,0,1),令平面A1CD的法向量是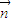 =(x,y,z),由于
=(x,y,z),由于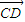 =(-2,4,0),
=(-2,4,0),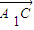 =(2,2,-4),
=(2,2,-4),
又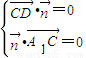 ,故有
,故有 ,令y=1,则x=2,z=1,故
,令y=1,则x=2,z=1,故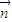 =(2,1,1)
=(2,1,1)
∴二面角A1-CD-A的余弦的大小为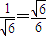
故二面角A1-CD-A的大小为arccos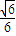
(理科):
(1)由图知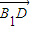 =(-2,6,-4),
=(-2,6,-4),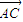 =(2,2,0),两向量夹角的余弦是
=(2,2,0),两向量夹角的余弦是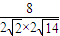 =
=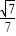
故异面直线B1D与直线AC所成角大小为arccos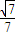 ;
;
(2)考察图形,三棱锥D-B1C1C的体积易得,故可用等体积法求解,
由于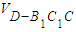 =
=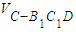
由图知,点D到面B1C1C的距离是2,三角形B1C1C的面积是4,故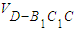 =
=
又点D到线B1C1的距离为2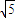 ,故三角形DB1C1的面积是
,故三角形DB1C1的面积是 ×2×2
×2×2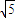 =2
=2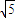
故点C到平面B1C1D的距离为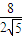 =
=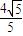
点评:本题考查异面直线所成的角和二面角及点到线的距离,本题解题的关键是建立坐标系,把立体几何理论推导变化成数字的运算,这样降低了题目的难度,但是不利于锻炼学生的理论推导能力.
(2)设出一个平面的法向量,根据向量垂直的条件,得到法向量的坐标之间的关系,写出其中一个,另一个平面上的法向量可以看出法向量,根据两个向量所成的角得到二面角.
(理科)(1)本题图形中出现了同一点出发的三条两两垂直的线段,故可以建立空间坐标系用向量法求解,写出要用的点的坐标,得到对应的异面直线的方向向量,根据向量所成的角得到结果.
(2)根据三棱锥D-B1C1C的体积易得,故可用等体积法求解,由于VD-B1C1C=VC-B1C1D,点D到面B1C1C的距离是2,三角形B1C1C的面积是4,又点D到线B1C1的距离为2
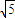 ,故三角形DB1C1的面积可得,代入求出点到面的距离
,故三角形DB1C1的面积可得,代入求出点到面的距离解答:
 解:直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,故可解得此棱柱的高是4
解:直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,故可解得此棱柱的高是4如图,以AB所在直线为X轴,以AD所在直线为Y轴,以AA1所在直线为Z轴建立空间坐标系,由上知A(0,0,0),B(2,0,0),C(2,2,0),D(0,6,0),A1(0,0,4),B1(2,0,4),C1(2,2,4),D1(0,6,4)
(文科):
(1)由题意
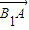 =(-2,0,-4),
=(-2,0,-4),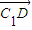 =(-2,4,-4)
=(-2,4,-4)两向量夹角的余弦值为
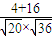 =
=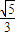
故两直线所成的角为arccos
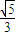
(2)由于面ACD是坐标平面,故其法向量可设为(0,0,1),令平面A1CD的法向量是
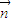 =(x,y,z),由于
=(x,y,z),由于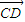 =(-2,4,0),
=(-2,4,0),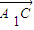 =(2,2,-4),
=(2,2,-4),又
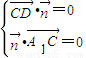 ,故有
,故有 ,令y=1,则x=2,z=1,故
,令y=1,则x=2,z=1,故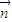 =(2,1,1)
=(2,1,1)∴二面角A1-CD-A的余弦的大小为
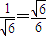
故二面角A1-CD-A的大小为arccos
(理科):
(1)由图知
 =(-2,6,-4),
=(-2,6,-4),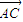 =(2,2,0),两向量夹角的余弦是
=(2,2,0),两向量夹角的余弦是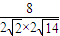 =
=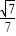
故异面直线B1D与直线AC所成角大小为arccos
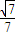 ;
;(2)考察图形,三棱锥D-B1C1C的体积易得,故可用等体积法求解,
由于
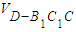 =
=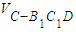
由图知,点D到面B1C1C的距离是2,三角形B1C1C的面积是4,故
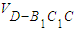 =
=
又点D到线B1C1的距离为2
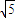 ,故三角形DB1C1的面积是
,故三角形DB1C1的面积是 ×2×2
×2×2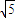 =2
=2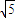
故点C到平面B1C1D的距离为
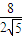 =
=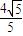
点评:本题考查异面直线所成的角和二面角及点到线的距离,本题解题的关键是建立坐标系,把立体几何理论推导变化成数字的运算,这样降低了题目的难度,但是不利于锻炼学生的理论推导能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.
已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD. 如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足
如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点. (2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.
(2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.