题目内容
若关于x的方程| x2-4 |
分析:由根据方程的根与对应函数零点之间的关系,我们可将方程
=x+m无实数解,转化为对应函数无零点,即函数y=
与函数y=x+m的图象无交点,利用图象法,我们易求出实数m的取值范围.
| x2-4 |
| x2-4 |
解答: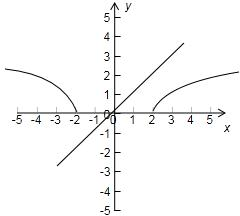 解:若方程
解:若方程
=x+m无实数解
则函数y=
与函数y=x+m的图象无交点
在同一坐标系中分别画出函数y=
与函数y=x+m的图象如下图所示:
∵y=
的图象是双曲线的一部分,
结合上图,我们易得满足条件的实数m的取值范围是[0,2)∪(-∞,-2)
故答案为[0,2)∪(-∞,-2).
 解:若方程
解:若方程 | x2-4 |
则函数y=
| x2-4 |
在同一坐标系中分别画出函数y=
| x2-4 |
∵y=
| x2-4 |
结合上图,我们易得满足条件的实数m的取值范围是[0,2)∪(-∞,-2)
故答案为[0,2)∪(-∞,-2).
点评:本题考查的知识点是直线和圆的方程的应用,其中根据方程的根与对应函数零点之间的关系,将问题转化为函数的零点问题是解答本题的关键.

练习册系列答案
相关题目
△ABC中三个内角为A、B、C,若关于x的方程x2-xcosAcosB-cos2
=0有一根为1,则△ABC一定是( )
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |