题目内容
(12分)求过点P(6,-4)且被圆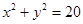 截得长为
截得长为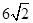 的弦所在的直线方程.
的弦所在的直线方程.
【答案】
 或
或
【解析】
试题分析:设弦所在的直线方程为 ,即
,即 ①
①
则圆心(0,0)到此直线的距离为 .
.
因为圆的半弦长、半径、弦心距恰好构成Rt△,
所以 .
.
由此解得 或
或 .
.
代入①得切线方程 或
或
 ,即
,即 或
或 .
.

考点:本题主要考查直线与圆的位置关系、直线方程。
点评:研究直线与圆的位置关系,可根据条件灵活选用“代数法”或‘几何法。圆的半弦长、半径、弦心距构成Rt△,在解“弦问题”中常常用到。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ;(3)求过点P(3,-6)与函数f(x)的图像相切的直线方程。(12分)
;(3)求过点P(3,-6)与函数f(x)的图像相切的直线方程。(12分)
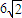 的弦所在的直线方程.
的弦所在的直线方程.