Question

“OA∥O₁A₁，OB∥O₁B₁”是“∠AOB=∠A₁O₁B₁”的（　　）

A．充要条件

B．充分不必要条件

C．必要不充分条件

D．既不充分又不必要条件

Answer 1

分析：结合直线平行的性质，利用充分条件和必要条件的定义进行判断．

解答：解：在空间中，当“OA∥O₁A₁，OB∥O₁B₁”，则“∠AOB=∠A₁O₁B₁”或“∠AOB=π-∠A₁O₁B₁”，所以不成立．如图1．
同理当“∠AOB=∠A₁O₁B₁”时，也无法得到OA∥O₁A₁，OB∥O₁B₁”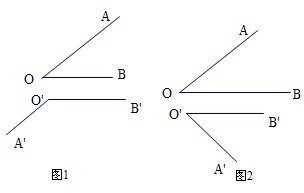，如图2．
所以“OA∥O₁A₁，OB∥O₁B₁”是“∠AOB=∠A₁O₁B₁”的既不充分又不必要条件．
故选D．

点评：本题主要考查充分条件和必要条件的判断，比较基础．