题目内容
已知定义在 上的函数
上的函数 满足
满足 .当
.当 时
时 .设
.设 在
在 上的最大值为
上的最大值为 ,且数列
,且数列 的前
的前 项和为
项和为 ,则
,则 . (其中
. (其中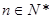 )
)
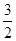
解析试题分析:依题意可得函数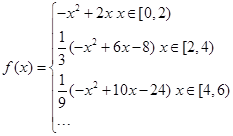 .所以
.所以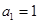 ,
,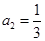 ,
,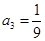 ,…,
,…,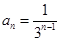 .所以数列
.所以数列 是一个首项为1,公比为
是一个首项为1,公比为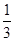 的等比数列.所以
的等比数列.所以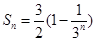 .所以
.所以
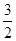 .
.
考点:1.函数的性质.2.数列的通项.3.函数的最值.4.极限问题.

练习册系列答案
相关题目
设 是将函数
是将函数 向左平移
向左平移 个单位得到的,则
个单位得到的,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
“三角函数是周期函数,y=tanx,x∈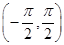 是三角函数,所以y=tan x,
是三角函数,所以y=tan x,
x∈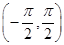 是周期函数.”在以上演绎推理中,下列说法正确的是( ).
是周期函数.”在以上演绎推理中,下列说法正确的是( ).
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
已知函数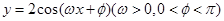 满足
满足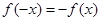 ,其图像与直线y=0的某两个交点的横坐标分别为
,其图像与直线y=0的某两个交点的横坐标分别为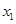 、
、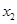 ,
,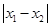 的最小值为
的最小值为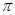 ,则( ).
,则( ).
A.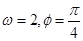 | B. | C.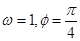 | D. |
若 是定义在R上的连续函数,且
是定义在R上的连续函数,且 ,则
,则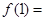 ( )
( )
| A.2 | B.1 | C.0 | D.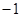 |
设函数f(x)=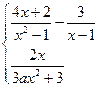
 在点x=1处连续,则a等于
在点x=1处连续,则a等于
A.-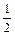 | B.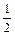 | C.-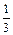 | D.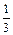 |
已知映射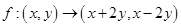 ,在映射
,在映射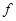 下
下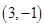 的原象是( )
的原象是( )
A.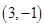 | B.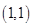 | C.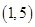 | D.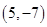 |
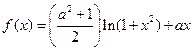

 .
.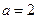 时,求
时,求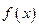 的极值
的极值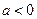 时,讨论
时,讨论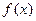 的单调性。
的单调性。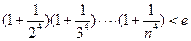 (
(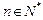 ,
,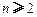 ,其中无理数
,其中无理数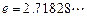 )
) ,则
,则 .
.