Question

设常数，函数，.

（Ⅰ）令，求的最小值，并比较的最小值与零的大小；

（Ⅱ）求证：在上是增函数；

（Ⅲ）求证：当时，恒有．

Answer 1

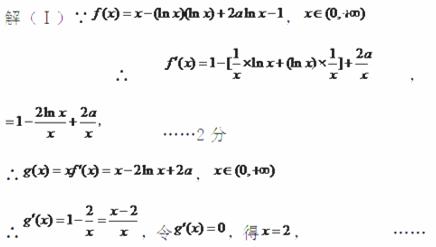
3分

列表如下：

		2
		0
	↘	极小值	↗

∴在处取得极小值，

即的最小值为．               ……5分

，

∵，∴，又，∴．         ……7分

证明（Ⅱ）由（Ⅰ）知，的最小值是正数，

∴对一切，恒有，           ……9分

从而当时，恒有，                    

故在上是增函数．                       ……11分

证明（Ⅲ）由（Ⅱ）知：在上是增函数，

     ∴当时，，                           ……12分

     又，                      ……13分

∴，即，             

∴

故当时，恒有．