题目内容
对于任意两个正整数,定义运算(用⊕表示运算符号):当m,n都是正偶数或都是正奇数时,m⊕n=m+n;而当m,n中一个为正偶数,另一个为正奇数时,m⊕n=m×n.例如4⊕6=4+6=10,3⊕7=3+7=10,3⊕4=3×4=12.在上述定义中,集合M={(a,b)|a⊕b=12,a,b∈N*}的元素有________个.
15
分析:由⊕的定义,a⊕b=12分两类进行考虑:a和b一奇一偶,则ab=12;a和b同奇偶,则a+b=12.由a、b∈N*列出满足条件的所有可能情况,再考虑点(a,b)的个数即可.
解答:a⊕b=36,a、b∈N*,
若a和b一奇一偶,则ab=12,满足此条件的有1×12=3×4,故点(a,b)有4个;
若a和b同奇偶,则a+b=12,满足此条件的有1+11=2+10=3+9=4+8=5+7=6+6共6组,故点(a,b)有2×6-1=11个,
所以满足条件的个数为4+11=15个.
故答案为:15
点评:本题为新定义问题,考查对新定义和集合的理解,正确理解新定义的含义是解决本题的关键.
分析:由⊕的定义,a⊕b=12分两类进行考虑:a和b一奇一偶,则ab=12;a和b同奇偶,则a+b=12.由a、b∈N*列出满足条件的所有可能情况,再考虑点(a,b)的个数即可.
解答:a⊕b=36,a、b∈N*,
若a和b一奇一偶,则ab=12,满足此条件的有1×12=3×4,故点(a,b)有4个;
若a和b同奇偶,则a+b=12,满足此条件的有1+11=2+10=3+9=4+8=5+7=6+6共6组,故点(a,b)有2×6-1=11个,
所以满足条件的个数为4+11=15个.
故答案为:15
点评:本题为新定义问题,考查对新定义和集合的理解,正确理解新定义的含义是解决本题的关键.

练习册系列答案
相关题目
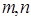 ,定义某种运算“※”如下:当
,定义某种运算“※”如下:当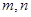 都为正偶数或正奇数时,
都为正偶数或正奇数时, 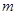 ※
※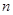 =
=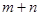 ;当
;当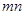 .则在此定义下,集合
.则在此定义下,集合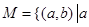 ※
※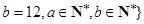 中的元素个数是( )
中的元素个数是( )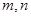 ,定义某种运算 “※”如下:当
,定义某种运算 “※”如下:当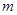 ※
※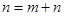 ;当
;当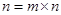 .则在此定义下,集合
.则在此定义下,集合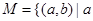 ※
※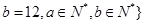 中的元素个数是 ( )
中的元素个数是 ( )