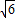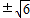题目内容
已知2a=3b=m,且
+
=2,则实数m的值为
.
| 1 |
| a |
| 1 |
| b |
| 6 |
| 6 |
分析:由已知中2a=3b=m,结合指数式和对数式的互化方法和换底公式的变形,可得
=logm2,
=logm3,进而根据
+
=2,可构造关于m的对数方程,解方程可得答案.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
解答:解:∵2a=3b=m
∴
=logm2,
=logm3,
又∵
+
=2
即logm2+logm3=logm6=2
解得m=
故答案为:
∴
| 1 |
| a |
| 1 |
| b |
又∵
| 1 |
| a |
| 1 |
| b |
即logm2+logm3=logm6=2
解得m=
| 6 |
故答案为:
| 6 |
点评:本题考查的知识点是换底公式的应用,指数式与对数式的互化,其中根据已知条件得到
=logm2,
=logm3,是解答本题的关键.
| 1 |
| a |
| 1 |
| b |

练习册系列答案
相关题目
已知2a=3b=m,且
+
=2,则实数m的值为( )
| 1 |
| a |
| 1 |
| b |
A、
| ||
B、
| ||
| C、6 | ||
D、±
|
 ,则实数m的值为( )
,则实数m的值为( )