题目内容
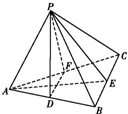 三棱锥P-ABC的所有棱长都相等,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是
三棱锥P-ABC的所有棱长都相等,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是
- A.BC∥平面PDF
- B.DF⊥平面PAE
- C.平面PDF⊥平面ABC
- D.平面PAE⊥平面ABC
C
分析:A.利用三角形的中位线定理可得BC∥DF,再利用线面平行的判定定理可得BC∥平面PDF,故A正确;
B.D.由等腰三角形的性质可得BC⊥AE,BC⊥PE,利用线面垂直的判定定理得BC⊥平面PAE,进而得到DF⊥平面PAE,再利用面面垂直的性质定理得平面PAE⊥平面ABC,故B、D都正确.
利用排除法可得,C不正确.
解答:A.∵D、F分别是AB、CA的中点,由三角形的中位线定理可得:BC∥DF,
∵BC?平面PDF,DF?平面PDF,∴BC∥平面PDF,故A正确;
B.D.∵AC=AB,BE=EC,∴BC⊥AE.
同理BC⊥PE,
∵PE∩AE=E,∴BC⊥平面PAE,
∵BC∥DF,∴DF⊥平面PAE,
∵DF?平面ABC,
∴平面PAE⊥平面ABC,
故B、D都正确.
排除A,B,D,故C不正确.
故选C.
点评:熟练掌握等腰三角形的性质、三角形的中位线定理、线面与面面垂直的判定和性质定理即可得出.
分析:A.利用三角形的中位线定理可得BC∥DF,再利用线面平行的判定定理可得BC∥平面PDF,故A正确;
B.D.由等腰三角形的性质可得BC⊥AE,BC⊥PE,利用线面垂直的判定定理得BC⊥平面PAE,进而得到DF⊥平面PAE,再利用面面垂直的性质定理得平面PAE⊥平面ABC,故B、D都正确.
利用排除法可得,C不正确.
解答:A.∵D、F分别是AB、CA的中点,由三角形的中位线定理可得:BC∥DF,
∵BC?平面PDF,DF?平面PDF,∴BC∥平面PDF,故A正确;
B.D.∵AC=AB,BE=EC,∴BC⊥AE.
同理BC⊥PE,
∵PE∩AE=E,∴BC⊥平面PAE,
∵BC∥DF,∴DF⊥平面PAE,
∵DF?平面ABC,
∴平面PAE⊥平面ABC,
故B、D都正确.
排除A,B,D,故C不正确.
故选C.
点评:熟练掌握等腰三角形的性质、三角形的中位线定理、线面与面面垂直的判定和性质定理即可得出.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
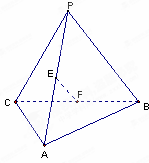 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、60° | B、45° | C、0° | D、120° |
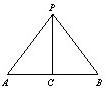 已知一个正三棱锥P-ABC的主视图如图所示,若AC=BC=
已知一个正三棱锥P-ABC的主视图如图所示,若AC=BC=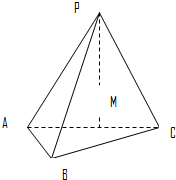 如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.
如图在三棱锥P-ABC中,PA=PB=PC=13,∠ABC=90°,AB=8,BC=6,M为AC的中点.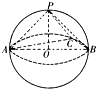 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC, (2013•嘉定区一模)如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,AC=BC=PA=2.
(2013•嘉定区一模)如图,在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,AC=BC=PA=2.