题目内容
在某高中数学竞赛附加试卷中只有三道题,已知:该校25个学生参加竞赛,每个学生至少解出一道题;在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍;只解出第一题的学生比余下的学生中解出第一题的人数多1人;只解出一道题的学生中,有一半没有解出第一题,则共有多少学生只解出第二题?
分析:先设出集合和集合的元素个数,根据原题中的条件列出方程,化简方程,确定所求解的未知数的范围,再结合元素的个数为正整数这一特点,即可得解
解答:解:设解出甲、乙、丙三题的学生的集合分别为A、B、C,并用三个圆表示之,则重叠部分表示同时解出两题或三题的学生的集合,其人数分别以a,b,c,d,e,f,g表示.
由于每个学生至少解出一题,故a+b+c+d+e+f+g=25①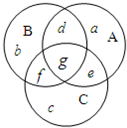
由于没有解出甲题的学生中,解出乙题的人数是解出丙题的人数的2倍,
故b+f=2(c+f)②
由于只解出甲题的学生比余下的学生中解出甲题的学生的人数多1,故a=d+e+g+1③
由于只解出一题的学生中,有一半没有解出甲题,故a=b+c④
由②得:b=2c+f,f=b-2c⑤
以⑤代入①消去f得a+2b-c+d+e+g=25⑥
以③、④分别代入⑥得:2b-c+2d+2e+2g=24⑦
3b+d+e+g=25⑧
以2×⑧-⑦得:4b+c=26⑨
∵c≥0,∴4b≤26,b≤6
.
利用⑤⑨消去c,得f=b-2(26-4b)=9b-52
∵f≥0,∴9b≥52,b≥
.
∵b∈Z,
∴b=6.即只解出乙题的学生有6人.
由于每个学生至少解出一题,故a+b+c+d+e+f+g=25①

由于没有解出甲题的学生中,解出乙题的人数是解出丙题的人数的2倍,
故b+f=2(c+f)②
由于只解出甲题的学生比余下的学生中解出甲题的学生的人数多1,故a=d+e+g+1③
由于只解出一题的学生中,有一半没有解出甲题,故a=b+c④
由②得:b=2c+f,f=b-2c⑤
以⑤代入①消去f得a+2b-c+d+e+g=25⑥
以③、④分别代入⑥得:2b-c+2d+2e+2g=24⑦
3b+d+e+g=25⑧
以2×⑧-⑦得:4b+c=26⑨
∵c≥0,∴4b≤26,b≤6
| 1 |
| 2 |
利用⑤⑨消去c,得f=b-2(26-4b)=9b-52
∵f≥0,∴9b≥52,b≥
| 52 |
| 9 |
∵b∈Z,
∴b=6.即只解出乙题的学生有6人.
点评:本题重点考查合情推理,考查用Venn图解决集合问题,利用条件构建方程,确定未知数范围是关键.属中档题

练习册系列答案
相关题目