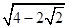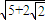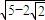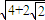题目内容
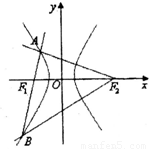
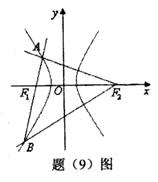
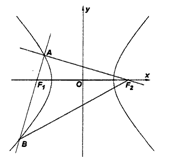
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )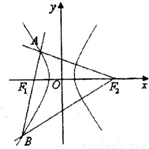
A.
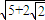
B.
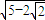
C.

D.
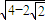
【答案】分析:设AF2=m,AF1=x,根据双曲线的基本性质及△ABF2是等腰三角形,用m分别表示出x,a,c,进而求得离心率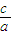 .
.
解答:解:设AF2=m,AF1=x
又AB=AF2,则BF1=m-x=2a,BF2=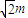 .
.
BF2-BF1=2a,即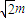 -2a=2a,故a=
-2a=2a,故a=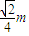 ,
,
又 m-x=2a,解得 x=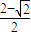 m,
m,
在△AF1F2中,由勾股定理知,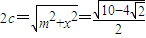 m
m
所以双曲线的离心率e=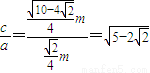
故选B.
点评:本题考查了双曲线的基本性质及其灵活运用,属于中档题型.
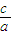 .
.解答:解:设AF2=m,AF1=x
又AB=AF2,则BF1=m-x=2a,BF2=
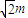 .
.BF2-BF1=2a,即
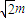 -2a=2a,故a=
-2a=2a,故a=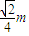 ,
,又 m-x=2a,解得 x=
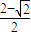 m,
m,在△AF1F2中,由勾股定理知,
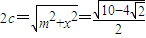 m
m所以双曲线的离心率e=
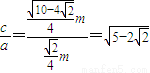
故选B.
点评:本题考查了双曲线的基本性质及其灵活运用,属于中档题型.

练习册系列答案
相关题目
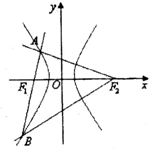 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
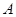 作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点
作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点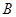 ,若
,若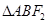 是等腰三角形,则双曲线的离心率为( )
是等腰三角形,则双曲线的离心率为( )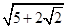 B.
B.
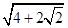 D.
D.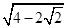
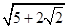 B.
B.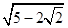 C.
C.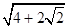 D.
D.