题目内容
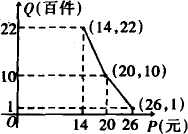
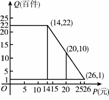
在对口扶贫活动中,企业甲将经营状况良好的某种消费品专卖店以优惠价格转让给了小型残疾人企业乙,并约定从该店经营的利润中逐步偿还(不计利息).在甲提供的资料中有:①这种消费品的进价为每件30元;②该店日销售量Q(件)与销售单价x(元/件)的关系是: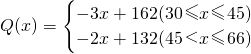 ;③该店每日所需各项开支为120元.
;③该店每日所需各项开支为120元.
(1)写出企业乙每日的经营利润函数f(x);
(2)当商品每件单价为多少元时,函数f(x)有最大值?并求出此最大值.
解:(1)企业乙每日的经营利润为该店日销售利润,减去该店每日所需各项开支
∵这种消费品的进价为每件30元,该店日销售量Q(件)与销售单价x(元/件)的关系是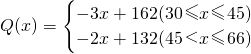 ,
,
∴该店日销售利润为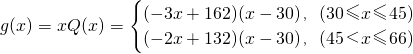
∴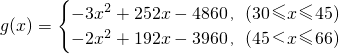
∴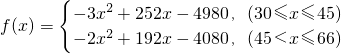
(2)当30≤x≤45时,f(x)=-3x2+252x-4980=-3(x-42)2+312
∴x=42时,函数的最大值为312
当45<x≤66时,f(x)=-2x2+192x-4080=-2(x-48)2+528
∴x=48时,函数的最大值为528
综上知,商品每件单价为48元时,函数f(x)有最大值,最大值为528.
分析:(1)企业乙每日的经营利润为该店日销售利润,减去该店每日所需各项开支,根据条件,先求出该店日销售利润,进而可求企业乙每日的经营利润函数f(x);
(2)利用配方法,分段求出函数的最值,比较其结果,确定函数f(x)的最大值.
点评:本题主要考查了分段函数的解析式,以及分段函数的最值和函数模型的选择与应用,同时考查计算能力,函数模型的构建是关键,属于中档题.
∵这种消费品的进价为每件30元,该店日销售量Q(件)与销售单价x(元/件)的关系是
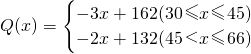 ,
,∴该店日销售利润为
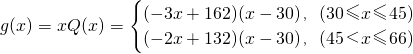
∴
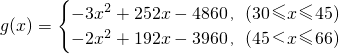
∴
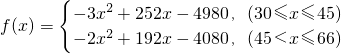
(2)当30≤x≤45时,f(x)=-3x2+252x-4980=-3(x-42)2+312
∴x=42时,函数的最大值为312
当45<x≤66时,f(x)=-2x2+192x-4080=-2(x-48)2+528
∴x=48时,函数的最大值为528
综上知,商品每件单价为48元时,函数f(x)有最大值,最大值为528.
分析:(1)企业乙每日的经营利润为该店日销售利润,减去该店每日所需各项开支,根据条件,先求出该店日销售利润,进而可求企业乙每日的经营利润函数f(x);
(2)利用配方法,分段求出函数的最值,比较其结果,确定函数f(x)的最大值.
点评:本题主要考查了分段函数的解析式,以及分段函数的最值和函数模型的选择与应用,同时考查计算能力,函数模型的构建是关键,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 ;③该店每日所需各项开支为120元.
;③该店每日所需各项开支为120元.