题目内容
x∈(0,2),则y=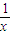 +
+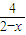 的最小值是 .
的最小值是 .
【答案】分析:由题意可得,y= +
+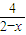 =
= (
( +
+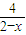 )[x+(2-x)]=
)[x+(2-x)]= [5+
[5+ ],利用基本不等式可求函数的最小值
],利用基本不等式可求函数的最小值
解答:解:∵0<x<2
∴0<2-x<2
则y=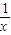 +
+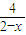 =
= (
(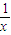 +
+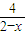 )[x+(2-x)]
)[x+(2-x)]
= [5+
[5+ ]
]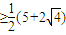 =
=
当且仅当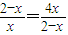 即x=
即x= 时取等号
时取等号
故答案为:
点评:本题主要考查了利用基本不等式求解函数的最值,解题的关键是灵活利用x+(2-x)=2的条件
 +
+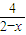 =
= (
( +
+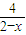 )[x+(2-x)]=
)[x+(2-x)]= [5+
[5+ ],利用基本不等式可求函数的最小值
],利用基本不等式可求函数的最小值解答:解:∵0<x<2
∴0<2-x<2
则y=
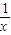 +
+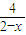 =
= (
(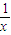 +
+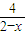 )[x+(2-x)]
)[x+(2-x)]=
 [5+
[5+ ]
]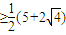 =
=
当且仅当
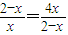 即x=
即x= 时取等号
时取等号故答案为:

点评:本题主要考查了利用基本不等式求解函数的最值,解题的关键是灵活利用x+(2-x)=2的条件

练习册系列答案
相关题目