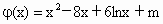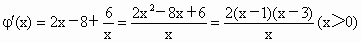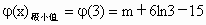题目内容
(2006
福建,21)已知函数 ,
, .
.
(1)
求f(x)在区间[t,t+1]上的最大值h(t);(2)
是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由.
答案:略
解析:
提示:
解析:
|
解析: (1)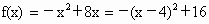 ,当t+1<4,即t<3时,f(x)在[t,t+1]上单调递增, ,当t+1<4,即t<3时,f(x)在[t,t+1]上单调递增,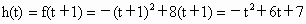 ;当t≤4≤t+1,即3≤t≤4时,h(t)=f(4)=16; ;当t≤4≤t+1,即3≤t≤4时,h(t)=f(4)=16;
当 t>4时,f(x)在[t,t+1]上单调递减, . .
综上, 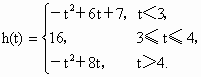
(2) 函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点,即函数φ(x)=g(x)-f(x)的图象与x轴的正半轴有且只有三个不同的交点.∵ ∴ 当 x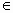 (0,1)时, (0,1)时,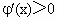 ,φ(x)是增函数; ,φ(x)是增函数;
当 x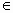 (1,3)时, (1,3)时,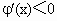 ,φ(x)是减函数; ,φ(x)是减函数;
当 x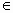 (3,+∞)时, (3,+∞)时,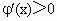 ,φ(x)是增函数; ,φ(x)是增函数;
当 x=1,或x=3时, . .
∴
∵ 当x充分接近0时,φ(x)<0,当x充分大时,φ(x)>0.∴ 要使φ(x)的图象与x轴正半轴有三个不同的交点,必须且只需
即 7<m<15-61n3.所以存在实数 m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3). |
提示:
|
剖析:本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力. |

练习册系列答案
相关题目