题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为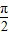 ,且图象上一个最低点为M(
,且图象上一个最低点为M( ,-2).
,-2).(1)求f(x)的解析式;
(2)用“五点法”画出函数f(x)的简图;
(3)求f(x)的单调增区间;
(4)求f(x)的对称轴方程、对称点坐标.
【答案】分析:(1)直接求出函数的周期T,A以及ω,通过函数经过的特殊点求出φ,得到函数的解析式;
(2)根据函数的解析式,通过列表,描点,连线画出函数的图象.
(3)利用正弦函数的单调增区间,求出f(x)的单调增区间;
(4)根据正弦函数的对称轴方程,求出函数的对称轴方程,利用正弦函数的对称中心求出函数的对称中心坐标即可.
解答:解:(1)由题意可知,T=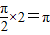 ,A=2,ω=
,A=2,ω=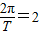 ,
,
∵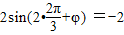 ,∴φ=
,∴φ=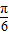 +2kπ,k∈Z,∵
+2kπ,k∈Z,∵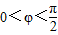
∴φ=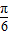
所以函数:f(x)=2sin(2x+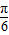 ).
).
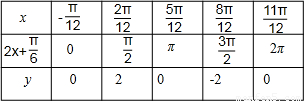
(2)f(x)=2sin(2x+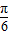 ).
).
列表
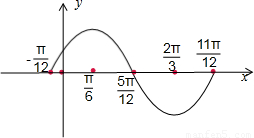
(3)因为ysinx的单调增区间为:[-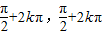 ]k∈Z
]k∈Z
所以f(x)=2sin(2x+ ) 可得
) 可得
-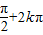 ≤2x+
≤2x+ ≤
≤
解得 x∈[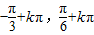 ]k∈Z
]k∈Z
f(x)的单调增区间:[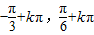 ]k∈Z
]k∈Z
(5)函数f(x)=2sin(2x+ ).因为2x+
).因为2x+ =kπ+
=kπ+ ,k∈Z所以函数的对称轴方程为:x=
,k∈Z所以函数的对称轴方程为:x= ,k∈Z
,k∈Z
因为2x+ =kπ,k∈Z所以函数的对称中心坐标为:(
=kπ,k∈Z所以函数的对称中心坐标为:(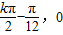 ),k∈Z.
),k∈Z.
点评:本题是中档题,考查三角函数的解析式的求法,五点法作图,函数的单调性的应用,函数图象的平移伸缩变换,函数的最值,可以说一题概括三角函数的基本知识的灵活应用,考查计算能力.
(2)根据函数的解析式,通过列表,描点,连线画出函数的图象.
(3)利用正弦函数的单调增区间,求出f(x)的单调增区间;
(4)根据正弦函数的对称轴方程,求出函数的对称轴方程,利用正弦函数的对称中心求出函数的对称中心坐标即可.
解答:解:(1)由题意可知,T=
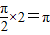 ,A=2,ω=
,A=2,ω=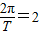 ,
,∵
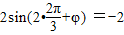 ,∴φ=
,∴φ=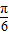 +2kπ,k∈Z,∵
+2kπ,k∈Z,∵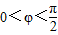
∴φ=
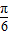
所以函数:f(x)=2sin(2x+
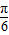 ).
).(2)f(x)=2sin(2x+
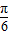 ).
).列表


(3)因为ysinx的单调增区间为:[-
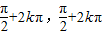 ]k∈Z
]k∈Z所以f(x)=2sin(2x+
 ) 可得
) 可得-
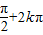 ≤2x+
≤2x+ ≤
≤
解得 x∈[
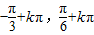 ]k∈Z
]k∈Zf(x)的单调增区间:[
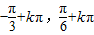 ]k∈Z
]k∈Z(5)函数f(x)=2sin(2x+
 ).因为2x+
).因为2x+ =kπ+
=kπ+ ,k∈Z所以函数的对称轴方程为:x=
,k∈Z所以函数的对称轴方程为:x= ,k∈Z
,k∈Z因为2x+
 =kπ,k∈Z所以函数的对称中心坐标为:(
=kπ,k∈Z所以函数的对称中心坐标为:(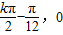 ),k∈Z.
),k∈Z.点评:本题是中档题,考查三角函数的解析式的求法,五点法作图,函数的单调性的应用,函数图象的平移伸缩变换,函数的最值,可以说一题概括三角函数的基本知识的灵活应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目