题目内容
若椭圆和双曲线有相同焦点F1,F2,点P是两条曲线的一个公共点,并且
•
=0,e1,e2分别为它们的离心率,则
+
的值是______.
| PF1 |
| PF2 |
| 1 | ||
|
| 1 | ||
|
由题意设焦距为2c,椭圆的长轴长2a,双曲线的实轴长为2m,不妨令P在双曲线的右支上
由双曲线的定义|PF1|-|PF2|=2m ①
由椭圆的定义|PF1|+|PF2|=2a ②
又∠F1PF2=900,故|PF1|2+|PF2|2=4c2 ③
①2+②2得|PF1|2+|PF2|2=2a2+2m2④
-①2+②2得|PF1||PF2|=a2-m2⑤
将④⑤代入③得a2+m2=c2,即
+
=1,即
+
=2
故答案为2
由双曲线的定义|PF1|-|PF2|=2m ①
由椭圆的定义|PF1|+|PF2|=2a ②
又∠F1PF2=900,故|PF1|2+|PF2|2=4c2 ③
①2+②2得|PF1|2+|PF2|2=2a2+2m2④
-①2+②2得|PF1||PF2|=a2-m2⑤
将④⑤代入③得a2+m2=c2,即
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
故答案为2

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 和双曲线
和双曲线 有相同的焦点
有相同的焦点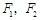 ,点
,点 是两条曲线的一个交点,则
是两条曲线的一个交点,则 的值为 .
的值为 . 和双曲线
和双曲线 有相同的焦点
有相同的焦点 、
、 ,P是两曲线的一个公共点,则
,P是两曲线的一个公共点,则 的值是( )
的值是( )
 D.
D.
 和双曲线
和双曲线 有相同的焦点
有相同的焦点 是椭圆与双曲线的一个交点,则
是椭圆与双曲线的一个交点,则 等于: ( )
等于: ( )
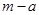 B.
B. C.
C. D.
D.
 和双曲线
和双曲线 有相同的左、右焦点
有相同的左、右焦点 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则 的值是( ).
的值是( ). B.
B.
 D.
D.