题目内容
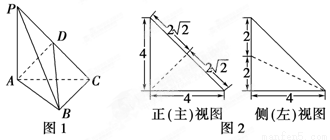
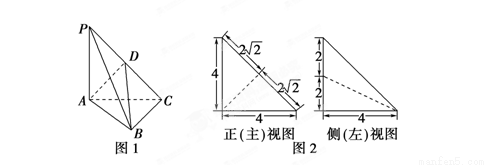
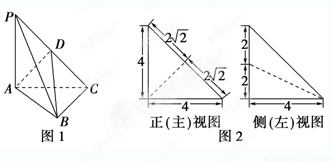
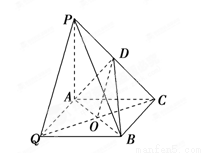
如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
【答案】
(1)根据线面垂直的判定定理,得到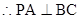 是解决该试题的关键。
是解决该试题的关键。
(2) (3)
(3)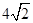
【解析】
试题分析:证明:(1)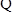
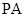
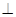 平面
平面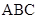 ,
,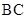
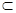
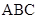
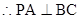
又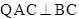 ,
,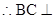 平面
平面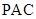
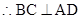
由三视图可得在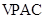 中
中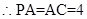
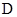 为
为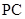 中点
中点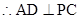 ,
, 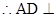 平面
平面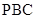
(2) 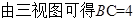
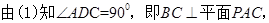
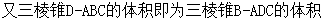
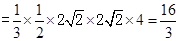 8分
8分
(3)取AB的中点O,连接CO并延长至Q,使得CQ=2CO,连接PQ,OD,点Q即为所求.
因为O为CQ的中点,D为PC的中点,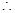 PQ//OD,
PQ//OD,
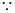 PQ
PQ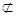 平面ABD, OD
平面ABD, OD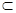 平面ABD
平面ABD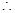 PQ//平面ABD
PQ//平面ABD
连接AQ,BQ, 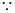 四边形ACBQ的对角线互相平分,且AC=BC,AC
四边形ACBQ的对角线互相平分,且AC=BC,AC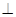 BC,
BC,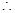 四边形ACBQ为正方形,
四边形ACBQ为正方形,
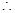 CQ即为∠ACB的平分线又
CQ即为∠ACB的平分线又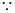 AQ=4,PA
AQ=4,PA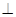 平面ABC
平面ABC
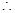 在直角三角形PAQ中,PQ=
在直角三角形PAQ中,PQ=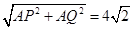 14分
14分
考点:空间中点线面的位置关系
点评:解决的关键是利用线面垂直的判定定理,以及锥体的体积公式和线面的平行的性质定理得到,属于基础题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
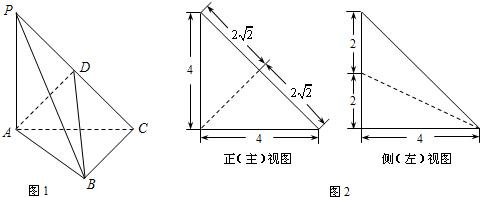
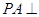 平面ABC,
平面ABC,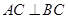 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。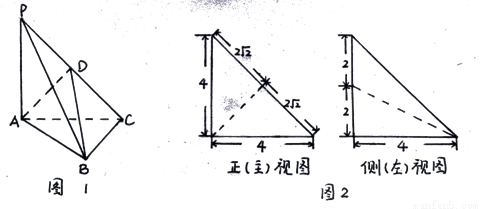
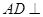 平面PBC;
平面PBC;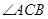 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得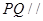 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。