题目内容
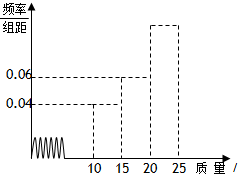 某集团在“5•12”地震灾区投资兴建了一条生产线生产三种不同规格的产品,现从生产线上随机抽取100件产品,得出频率分布直方图如下,
某集团在“5•12”地震灾区投资兴建了一条生产线生产三种不同规格的产品,现从生产线上随机抽取100件产品,得出频率分布直方图如下,其中质量在[10,15)之间的为A类产品,质量在[15,20)之间的为B类产品,质量在[20,25)之间的为C类产品,由市场行情知A、B、C三类产品的每件销售量利润分别为1元、2元、3元.
问:(1)抽取的100件样品中,C类产品的频数为
(2)若从生产线上随机抽取3件产品,求这3件产品销售利润和不小于7元的概率.
分析:(1)从频率分布直方图中可以看出C类产品的频率是1-5(0.04+0.06)=0.5从生产线上随机抽取100件产品.
(2)3件产品销售利润和不小于7元,包括三种情况即利润等于7元,利润等于8元,利润等于9元,写出事件对应的概率,根据互斥事件的概率得到结果.
(2)3件产品销售利润和不小于7元,包括三种情况即利润等于7元,利润等于8元,利润等于9元,写出事件对应的概率,根据互斥事件的概率得到结果.
解答:解:(1)从频率分布直方图中可以看出C类产品的频率是1-5(0.04+0.06)=0.5
∵从生产线上随机抽取100件产品,
∴0.5×100=50…(4分)
(2)设这3件产品的销售利润和为ξ
则P(ξ=7)=
(
)2(
)+
•(
)2=
…(6分)
P(ξ=8)=
•(
)2=
…(8分)
P(ξ=9)=
(
)3=
…(10分)
∴P(ξ≥7)=P(ξ=7)+P(ξ=8)+P(ξ=9)=
=0.635…(12分)
∵从生产线上随机抽取100件产品,
∴0.5×100=50…(4分)
(2)设这3件产品的销售利润和为ξ
则P(ξ=7)=
| C | 1 3 |
| 3 |
| 10 |
| 5 |
| 10 |
| C | 1 3 |
| 2 |
| 10 |
| 5 |
| 10 |
| 285 |
| 1000 |
P(ξ=8)=
| C | 1 3 |
| 3 |
| 10 |
| 5 |
| 10 |
| 225 |
| 1000 |
P(ξ=9)=
| C | 3 3 |
| 5 |
| 10 |
| 125 |
| 1000 |
∴P(ξ≥7)=P(ξ=7)+P(ξ=8)+P(ξ=9)=
| 635 |
| 1000 |
点评:题考查了对频数分布直方图的掌握情况,考查的是概率的求法和独立重复试验,本题解题的关键是理解正确读图,从图形中能够看出所要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
