题目内容
已知a是实数,函数f(x)=21nx+x2-ax(x∈(0,+∞)),
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与圆(x-1)2+y2=1相切,求a的值;
(Ⅱ)若函数f(x)在定义域上存在单调减区间,求a的取值范围;
(Ⅲ)若a=1,对 x1∈[1,e],
x1∈[1,e], x0∈[1,e]使f(x0)=m
x0∈[1,e]使f(x0)=m -x1成立,求m的取值范围。
-x1成立,求m的取值范围。
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与圆(x-1)2+y2=1相切,求a的值;
(Ⅱ)若函数f(x)在定义域上存在单调减区间,求a的取值范围;
(Ⅲ)若a=1,对
 x1∈[1,e],
x1∈[1,e], x0∈[1,e]使f(x0)=m
x0∈[1,e]使f(x0)=m -x1成立,求m的取值范围。
-x1成立,求m的取值范围。解:(Ⅰ) ,
, ,
,
又f(1)=1-a,切线方程:y-(1-a)=(4-a)(x-1),即(4-a)x-y-3=0,
又切线与圆(x-1)2+y2=1相切,得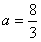 ;
;
(Ⅱ)若函数f(x)在定义域上存在单调减区间,(0,∞)使得f′(x)<0成立不等式 有正数解,
有正数解,
又x>0,故2x2-ax+2<0有解,
①当a<0不可能;
②当a>0时,Δ=a2-4a>0,a>4;
(Ⅲ)若a=1,对 使
使 成立;
成立;
f(x)在[1,e]上的值域为[0,e2-e+2]且g(x)= ,
,
g(1)∈[0,e2-e+2],m-1∈[0,e2-e+2],即m≥1,
 ,
,
故m的取值范围为e2≤m≤e2-e+3。
 ,
, ,
,又f(1)=1-a,切线方程:y-(1-a)=(4-a)(x-1),即(4-a)x-y-3=0,
又切线与圆(x-1)2+y2=1相切,得
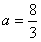 ;
; (Ⅱ)若函数f(x)在定义域上存在单调减区间,(0,∞)使得f′(x)<0成立不等式
 有正数解,
有正数解,又x>0,故2x2-ax+2<0有解,
①当a<0不可能;
②当a>0时,Δ=a2-4a>0,a>4;
(Ⅲ)若a=1,对
 使
使 成立;
成立;f(x)在[1,e]上的值域为[0,e2-e+2]且g(x)=
 ,
,g(1)∈[0,e2-e+2],m-1∈[0,e2-e+2],即m≥1,
 ,
,故m的取值范围为e2≤m≤e2-e+3。

练习册系列答案
相关题目