Question

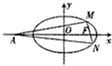（2012•西区模拟）已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

6

3

，F为椭圆的右焦点，M、N两点在椭圆C上，且

MF

=λ

FN

(λ＞0)，定点A（-4，0）．
（1）求证：当λ=1时，

MN

⊥

AF

；
（2）若当λ=1时，有

AM

•

AN

=

106

3

，求椭圆C的方程．

Answer 1

分析：（1）设M（x₁，y₁），N（x₂，y₂），F（c，0）通过λ=1时，

MF

=

FN

，M、N两点在椭圆上，求出x1 =x2 ，然后通过数量积证明

MN

⊥

AF

．
（2）当λ=1时，不妨设M（c，

b2

a

），N（c，-

b2

a

），通过λ=1时，有

AM

•

AN

=

106

3

，求出a，b，得到椭圆的方程．

解答：解：（1）证明：设M（x₁，y₁），N（x₂，y₂），F（c，0）
则

MF

=(c-x1，-y1)，

FN

=(x2-c，y2)，
当λ=1时，

MF

=

FN

∴-y₁=y₂，x₁+x₂=2c，
由M、N两点在椭圆上，
∴x12=a2(1-

y12

b2

)，x22=a2(1-

y22

b2

)，
∴x12=x22若
x1 =-x2 ，则x1 +x2 =0≠2，（舍去），
所以x1 =x2 ，
∴

MN

=(0，2y2)，

AF

=(4+c，0)，

MN

• 

AF

=0，
∴

MN

⊥

AF

．
（2）当λ=1时，不妨设M（c，

b2

a

），N（c，-

b2

a

），

AM

•

AN

=(c+4)2-

b4

a 2

= 

106

3

，
因为a²=

3

2

c2，b2=

1

2

c2，
∴

5

6

c2+8c+16=

106

3

，
∴c=2，a²=6，b²=2，
故椭圆的方程为

x2

6

+

y2

2

=1．

点评：本题考查椭圆的简单性质，向量在几何中的应用，椭圆的标准方程，考查函数与方程的思想，计算能力．