题目内容
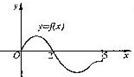 4、设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解是( )
4、设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解是( )分析:由奇函数图象的对称特征得出此函数在y轴左侧的图象特征,再结合图象,只须观察图象在x轴下方时相应的x的值即可解题.
解答:解:当x∈[0,5]时,由f(x)的图象可知,
x∈(0,2)时,不等式f(x)>0,
x∈(2,5]时,不等式f(x)<0
又奇函数f(x)的定义域为[-5,5]
故x∈(-2,0),不等式f(x)<0,
x∈[-5,-2))时,不等式f(x)>0.
则不等式f(x)<0的解是:(-2,0)∪(2,5].
故选D.
x∈(0,2)时,不等式f(x)>0,
x∈(2,5]时,不等式f(x)<0
又奇函数f(x)的定义域为[-5,5]
故x∈(-2,0),不等式f(x)<0,
x∈[-5,-2))时,不等式f(x)>0.
则不等式f(x)<0的解是:(-2,0)∪(2,5].
故选D.
点评:本题主要考查了奇偶函数图象的对称性,是数形结合思想运用的典范,解题要特别注意图中的区间的端点细节.

练习册系列答案
相关题目
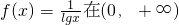 是减函数;
是减函数;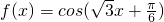 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;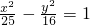 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;