题目内容
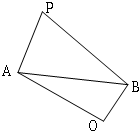如图，已知四边形PAOB中，PA⊥OA，PB⊥OB．且PA=5，PB=8，AB=7（1）求∠APB；
（2）求△APB的面积；
（3）求线段PO的长．
分析：（1）在△APB中，直接利用余弦定理求出∠APB的余弦函数值即可求出角的大小；
（2）直接一三角形的面积公式，求△APB的面积；
（3）利用三角形的外接圆的半径，以及正弦定理求线段PO的长
（2）直接一三角形的面积公式，求△APB的面积；
（3）利用三角形的外接圆的半径，以及正弦定理求线段PO的长
解答：解：（1）在△APB中，∵Cos∠APB=
=
=
∴∠APB=60°
（2）S△APB=
AP•PB•sinAPB=
×5×8×sin60°
=10
（3）线段PO即是△APB外接圆直径2R
而在△APB中，
=2R∴2R=
所以，线段PO的长为
| AP2+PB2-AB2 |
| 2AP•PB |
| 25+64-49 |
| 80 |
| 1 |
| 2 |
∴∠APB=60°
（2）S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
=10
| 3 |
（3）线段PO即是△APB外接圆直径2R
而在△APB中，
| AB |
| sinAPB |
14
| ||
| 3 |
14
| ||
| 3 |
点评：本题考查解三角形的知识，正弦定理与余弦定理三角形的面积公式的应用，基本知识的考查．
练习册系列答案
相关题目
17、如图，已知四边形ABCD 是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点．
如图，已知四边形ABCD是菱形，PA⊥平面ABCD，PA=AB=BD=2，AC与BD交于E点，F是PD的中点．
（2013•深圳二模）如图，已知四边形 ABCD 是矩形，AB=2BC=2，三角形 PAB 是正三角形，且 平面 ABCD⊥平面 PCD．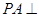
平面ABCD，PA=AB=BD=2，AC与BD交于E点，F是PD的中点。